Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Ta có:
y ' = − 3 x 2 + 4 x ; y ' = 1 ⇔ − 3 x 2 + 4 x = 1 ⇔ x = 1 x = 1 3 .
Khi x = 1, tiếp tuyến có phương trình y = x + 2 trùng với đường thẳng y = x + 2.
Khi x = , tiếp tuyến có phương trình y = x + 50 27 .

Đáp án D
Hệ số góc của tiếp tuyến tại điểm x 0 ; y 0 là:
k = y ' x 0 = − 4 x 0 − 2 2 = − 1 ⇔ x 0 = 0 x 0 = 4 ⇒ y 0 = − 1 y 0 = 3
Phương trình tiếp tuyến tại điểm 0 ; − 1 là: y + 1 = − x ⇔ x + y + 1 = 0
Phương trình tiếp tuyến tại điểm 4 ; 3 là: y − 3 = − 1 x − 4 ⇔ x + y − 7 = 0

Đáp án là C
y ' = − 2 x − 1 2 . Gọi M x 0 ; y 0 ∈ C là tiếp điểm.
Vì tiếp tuyến song song với đường thẳng y = − 2 x − 1 nên:
− 2 x 0 − 1 2 = − 2 ⇔ x 0 − 1 2 = 1 ⇔ x 0 = 2 ⇒ y 0 = 3 x 0 = 0 ⇒ y 0 = − 1
Phương trình tiếp tuyến cần tìm: 2 x + y − 7 = 0.

ta tính \(y'=3x^2\)
để tiếp tuyến của đồ thị hàm số song song với đường thẳng \(y=-3x+1\) thì \(y'\left(x_0\right)=\frac{-1}{-3}=\frac{1}{3}\) giả pt suy ra đc \(x_0=\pm\frac{1}{3}\)
TH1: \(x_0=\frac{1}{3}\) suy ra \(y_0=\frac{1}{27}+1=\frac{28}{27}\)
vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x-\frac{1}{3}\right)+\frac{28}{27}=\frac{1}{3}x+\frac{25}{27}\)
TH2:\(x_0=-\frac{1}{3}\) suy ra \(y_0=-\frac{1}{27}+1=\frac{26}{27}\)
vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x+\frac{1}{3}\right)+\frac{26}{27}=\frac{1}{3}x+\frac{29}{27}\)
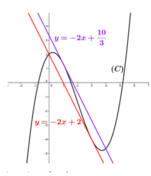







Đáp án B
Phương trình tiếp tuyến tại x 0 ; y 0 có hệ số góc là k = y ' = − 3 x − 1 2
Để tiếp tuyến tại x 0 ; y 0 song song với đường thẳng d : y = − 3 x − 1 thì
k = − 3 x − 1 2 = − 3 ⇔ x − 1 2 = 1 ⇔ x 1 = 2 x 2 = 0 ⇔ y 1 = 5 y 2 = − 1 ⇔ d 1 : y = − 3 x + 11 d 2 : y = − 3 x − 1 ≡ d ( l o a i )