
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

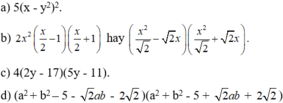

a, x^5+x^4+x^3-x^3-x²-x+x²+x+1
= x^3(x²+x+1)-x(x²+x+1)+1(x²+x+1)
= (x²+x+1).(x³-x²+1)

a) \(=[3\left(a-b\right)]^2-[2\left(x-y\right)]^2\)
\(=\left(3a-3b-2x+2y\right)\left(3a-3b+2x-2y\right)\)
b)\(=\left(a^2+3^2\right)^2-\left(6a\right)^2\)
\(=\left(a^2-2.a.3+3^2\right)\left(a^2+2.a.3+3^2\right)\)
\(=\left(a-3\right)^2.\left(a+3\right)^2\)
c)\(=\left(x+y\right)^2-2.\left(x+y\right).1+1^2\)
\(=\left(x+y-1\right)\left(x+y+1\right)\)
nhớ tích nha
\(9\left(a-b\right)^2-4\left(x-y\right)^2\)
\(=\left[3\left(a-b\right)\right]^2-\left[2\left(x-y\right)\right]^2\)
\(=\left(3a-3b\right)^2-\left(2x-2y\right)^2\)
\(=\left(3a-3b-2x+2y\right)\left(3a-3b+2x-2y\right)\)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

\(x^2-2x-4y^2-4y\)
\(=\left(x^2-4y^2\right)-\left(2x+4y\right)\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
\begin{array}{l} a){\left( {ab - 1} \right)^2} + {\left( {a + b} \right)^2}\\ = {a^2}{b^2} - 2ab + 1 + {a^2} + 2ab + {b^2}\\ = {a^2}{b^2} + 1 + {a^2} + {b^2}\\ = {a^2}\left( {{b^2} + 1} \right) + \left( {{b^2} + 1} \right)\\ = \left( {{a^2} + 1} \right)\left( {{b^2} + 1} \right)\\ c){x^3} - 4{x^2} + 12x - 27\\ = {x^3} - 27 + \left( { - 4{x^2} + 12x} \right)\\ = \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - 4x\left( {x - 3} \right)\\ = \left( {x - 3} \right)\left( {{x^2} + 3x + 9 - 4x} \right)\\ = \left( {x - 3} \right)\left( {{x^2} - x + 9} \right)\\ b){x^3} + 2{x^2} + 2x + 1\\ = {x^3} + 2{x^2} + x + x + 1\\ = x\left( {{x^2} + 2x + 1} \right) + \left( {x + 1} \right)\\ = x{\left( {x + 1} \right)^2} + \left( {x + 1} \right)\\ = \left( {x + 1} \right)\left( {x\left( {x + 1} \right) + 1} \right)\\ = \left( {x + 1} \right)\left( {{x^2} + x + 1} \right)\\ d){x^4} - 2{x^3} + 2x - 1\\ = {x^4} - 2{x^3} + {x^2} - {x^2} + 2x - 1\\ = {x^2}\left( {{x^2} - 2x + 1} \right) - \left( {{x^2} - 2x + 1} \right)\\ = \left( {{x^2} - 2x + 1} \right)\left( {{x^2} - 1} \right)\\ = {\left( {x - 1} \right)^2}\left( {x - 1} \right)\left( {x + 1} \right)\\ = {\left( {x - 1} \right)^3}\left( {x + 1} \right)\\ e){x^4} + 2{x^3} + 2{x^2} + 2x + 1\\ = {x^4} + 2{x^3} + {x^2} + {x^2} + 2x + 1\\ = {x^2}\left( {{x^2} + 2x + 1} \right) + \left( {{x^2} + 2x + 1} \right)\\ = \left( {{x^2} + 2x + 1} \right)\left( {{x^2} + 1} \right)\\ = {\left( {x + 1} \right)^2}\left( {{x^2} + 1} \right) \end{array} |

a.
\(25\left(x-y\right)^2-16\left(x+y\right)^2\)
\(=\left[5\left(x-y\right)\right]^2-\left[4\left(x+y\right)\right]^2\)
\(=\left[5\left(x-y\right)-4\left(x+y\right)\right]\left[5\left(x-y\right)+4\left(x+y\right)\right]\)
\(=\left(5x-5y-4x-4y\right)\left(5x-5y+4x+4y\right)\)
\(=\left(x-9y\right)\left(9x-y\right)\)
b.
\(\left(a^2+b^2-5\right)^2-4\left(ab+2\right)^2\)
\(=\left(a^2+b^2-5\right)^2-\left[2\left(ab+2\right)\right]^2\)
\(=\left[\left(a^2+b^2-5\right)+2\left(ab+2\right)\right]\left[\left(a^2+b^2-5\right)-2\left(ab+2\right)\right]\)
\(=\left(a^2+b^2-5+2ab+4\right)\left(a^2+b^2-5-2ab-4\right)\)
\(=\left[\left(a+b\right)^2-1\right]\left[\left(a-b\right)^2-9\right]\)
\(=\left[\left(a+b\right)^2-1^2\right]\left[\left(a-b\right)^2-3^2\right]\)
\(=\left(a+b-1\right)\left(a+b+1\right)\left(a-b-3\right)\left(a-b+3\right)\)

\(\left(x-5\right)^2-16=\left(x-5\right)^2-4^2=\left(x-5-4\right)\left(x-5+4\right)=\left(x-9\right)\left(x-1\right)\)
\(25-\left(3-x\right)^2=5^2-\left(3-x\right)^2=\left(5-3+x\right)\left(5+3-x\right)=\left(2+x\right)\left(8-x\right)\)
\(\left(7x-4\right)^2-\left(2x+1\right)^2=\left(7x-4-2x-1\right)\left(7x-4+2x+1\right)=\left(5x-5\right)\left(9x-3\right)=15\left(x-1\right)\left(3x-1\right)\)\(49\left(y-4\right)^2-9\left(y+2\right)^2=\left[7\left(y-4\right)\right]^2-\left[3\left(y+2\right)\right]^2=\left(7y-28-3y-6\right)\left(7y-28+3y-6\right)=\left(4y-34\right)\left(10y-22\right)\)\(=4.\left(2y-17\right)\left(5y-11\right)\)
e); f) Áp dụng hằng đẳng thức số 6,7 để làm

a, Dùng phương pháp đổi biến (đầu tiên ghép cặp (x+2) với (x+5) và cặp còn lại, rồi đổi biến)
b, Dùng phương pháp thêm bớt cùng 1 hạng tử
c, Dùng phương pháp nhóm hang tử

Bài1: Phân tích các đa thức sau thành nhân tử
a)36-4x2+4xy-y2
\(=6^2-\left(4x^2-4xy+y^2\right)\)
\(=6^2-\left(2x-y\right)^2\)
\(=\left(6+2x-y\right)\left(6-2x+y\right)\)
b)2x4+3x2-5
\(=2x^4-2x^2+5x^2-5\)
\(=2x^2\left(x^2-1\right)+5\left(x^2-1\right)\)
\(=\left(2x^2+5\right)\left(x^2-1\right)\)
\(=\left(2x^2+5\right)\left(x-1\right)\left(x+1\right)\)
B1:a)\(36-4x^2+4xy-y^2=36-\left(4x^2-4xy+y^2\right)=6^2-\left(2x-y\right)^2\)
\(=\left(6-2x+y\right)\left(6+2x-y\right)\)
c)\(a^3-ab^2+a^2+b^2-2ab=a\left(a^2-b^2\right)+\left(a-b\right)^2\)\(=a\left(a-b\right)\left(a+b\right)+\left(a-b\right)^2=\left(a-b\right)\left(a^2+ab+a-b\right)\)
d)\(x^2-\left(a^2+b^2\right)x+a^2b^2=x^2-a^2x-b^2x+a^2b^2\)\(=x\left(x-a^2\right)-b^2\left(x-a^2\right)=\left(x-a^2\right)\left(x-b^2\right)\)
e)\(x\left(x-y\right)+x^2-y^2=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)\(=\left(x-y\right)\left(x+x+y\right)=\left(x-y\right)\left(2x+y\right)\)

a)\(x^2+4x-4y^2-8y\)
\(=x^2+2xy+4x-2xy-4y^2-8y\)
\(=x\left(x+2y+4\right)-2y\left(x+2y+4\right)\)
\(=\left(x-2y\right)\left(x+2y+4\right)\)
b)sai đề
c)sai đề tiếp
a)x2+4x-4y2-8y=(x2-4y2)+(4x-8y)
=(x+2y(x-2y)+4(x-2y)
=(x-2y)(x+2y+4)