Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có ρ = 13 , 6 ( k g / d m 3 ) = 13 , 6 ( g / c m 3 )
Trạng thái 1 { V 1 = 14 ( c m 3 ) T 1 = 77 + 273 = 350 K Trạng thái 2 { V 2 T 2 = 273 + 27 = 300 K
Áp dụng định luật Gay – Luyxắc
V 1 V 2 = T 1 T 2 ⇒ V 2 = V 1 . T 2 T 1 = 14. 300 350 V 2 = 12 ( c m 2 )
Vậy lượng thể tích đã chảy vào bình là Δ V = V 1 − V 2 = 14 − 12 = 2 ( c m 3 )
Khối lượng thủy ngân chảy vào bình m = ρ . Δ V = 13 , 6.2 = 27 , 2 ( g )

+ Gọi V0 là thể tích của khối lập phương ở 0oC:
V0 = l03
+ V là thể tích của khối lập phương ở t0C:
V = l3 = [l0(1+ α∆t)]3 = l03 (1+α∆t)3
Mà (1+ α∆t)3 = 1 + 3α∆t + 3α2∆t2 + α3∆t3
Vì α khá nhỏ nên α2, α3 có thể bỏ qua.
=> V = l3 = l03 (1+ 3α∆t) = Vo (1+ β∆t) với β = 3α.

Ta có:
+ Khối lượng riêng: ρ = m V
Ở nhiệt độ 00C: ρ 0 = m V 0 (1)
Ở nhiệt độ 500C: ρ = m V
+ Mặt khác ta có: V = V 0 1 + β ∆ t = V 0 1 + 3 α ∆ t
Ta suy ra: ρ = m V 0 1 + β ∆ t (2)
Từ (1) và (2), ta suy ra: ρ ρ 0 = 1 1 + β ∆ t → ρ = ρ 0 1 + β ∆ t = 13600 1 + 1 , 82 . 10 - 4 . 50 = 13477 , 36 k g / m 3
Đáp án: B

V=0,197.10-3m3
S=0,2.10-4m2
khi tăng bình I lên nhiệt đô 30C
\(V_1=V+S.l\)
\(T_1=276K\)
khi giảm bình II còn -30C
\(V_2=V-S.l\)
\(T_2=270K\)
áp xuất bằng nhau khi giọt thủy ngân cân bằng
\(\frac{V_1}{T_1}=\frac{V_2}{T_2}\) ; \(\left(\frac{V_2}{T_2}=\frac{V}{T}=\frac{V_1}{T_1}\right)\)
\(\Leftrightarrow\frac{V+S.l}{276}=\frac{V-S.l}{270}\)
\(\Rightarrow l\approx\).........m
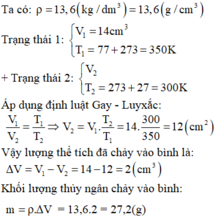
Gọi:
+ V0: thể tích của m0(kg) thủy ngân và của bình thủy tinh ở nhiệt độ 00C
+ V2: thể tích của bình thủy tinh ở nhiệt độ t1
+ V1: thể tích của m1(kg) thủy ngân ở nhiệt độ 00C
+ V2′: thể tích của m1 (kg) thủy ngân ở nhiệt độ t1
+ ρ: khối lượng riêng của thủy ngân.
Ta có:
Ta có: V 2 = V 2 ' (3)
Thay (1) và (2) vào (3), ta được:
Đáp án: B