Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
+ Độ lớn của trọng lực:
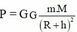
+ Gia tốc rơi tự do :

+ Nếu ở gần mặt đất (h << R) : ![]()
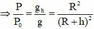
![]()

Ta có
Trọng lượng của vật ở mặt đất:
P = G m M R 2
Trọng lượng của vật ở độ cao h
P h = G m M R + h 2
Theo đề bài, ta có:
P h = 2 3 P ↔ G M m ( R + h ) 2 = 2 3 G M m R 2
⇔ 2 3 ( R + h ) 2 = R 2 ⇒ h = 0,225 R = 0,225.6400 = 1440 k m
Đáp án: C

Thế năng trọng trường Wt = mgh
= 1.10.9,8 = 98 (J)
Vậy vật có thể năng trọng trường là 98 (J).

Tính h?
\(g=\dfrac{GM}{R^2}=9,8\)
\(g'=\dfrac{GM}{\left(R+h\right)^2}=9,78\)
\(\Rightarrow\dfrac{9,8R^2}{\left(R+h\right)^2}=9,78\Leftrightarrow\dfrac{9,8.64.10^5}{\left(64.10^5+h\right)^2}=9,78\Rightarrow=h=...\left(m\right)\)

Chọn gốc thế năng tại mặt đất.
\(m=2kg\)
\(h=12m\)
\(g=10m/s^2\)
\(a,v=?\)
\(b,h'=?\) Khi \(W_d=2W_t\)
=========================
\(a,\) Ta có : \(W=W_d+W_t\)
\(=\dfrac{1}{2}mv^2+mgh\)
\(=\dfrac{1}{2}.2.0^2+2.10.12\)
\(=240\left(J\right)\)
Tại mặt đất : \(W_t=0\)
\(W_d=W=240J\)
Mà \(W_d=\dfrac{1}{2}mv^2\) \(\Leftrightarrow240=\dfrac{1}{2}.2.v^2\Leftrightarrow v=4\sqrt{15}\left(m/s\right)\)
\(b,\) \(W_d=2W_t\)
\(\Leftrightarrow\dfrac{1}{2}mv^2=2mgh'\)
\(\Leftrightarrow\dfrac{1}{2}.2.\left(4\sqrt{15}\right)^2=2.2.10.h'\)
\(\Leftrightarrow h'=6\left(m\right)\)

Độ lớn của trọng lực: P = G m . M R + h 2
Gia tốc rơi tự do : g h = G M R + h 2 ( 1 )
Nếu ở gần mặt đất (h << R) : P 0 = G m . M R 2 ; g 0 = G M R 2 ( 2 )
⇒ P P 0 = g h g = R 2 ( R + h ) 2 ⇒ g h = 0 , 04 g ⇒ P h = 8 N