
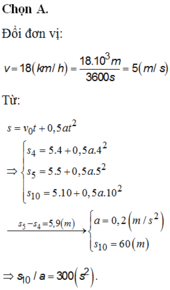
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

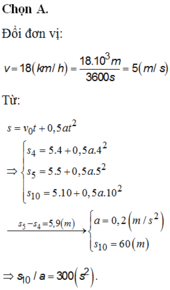

Theo kết quả trên, ta tìm được quãng đường vật đi được sau khoảng thời gian t = 10 s là
s 10 = 5.10 + (0.2. 10 2 )/2 = 50 + 10 = 60 (m)

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

bài 5
+Đổi vận tốc đầu: \(v_0=18km/h=5m/s\)
Quãng đường đi được trong thời gian t (kể từ t = 0): \(S=v_0t+\dfrac{at^2}{2}=5t+\dfrac{at^2}{2}\)
Quãng đường đi được trong 5 giây đầu (t = 5 s)
\(S_5=5.5+\dfrac{5^2a}{2}\)
Quãng đường đi được trong 4 giây đầu (t = 4 s):\(S_4=5.4+\dfrac{4^2a}{2}\)
Quãng đường đi được trong giây thứ 5:
\(\Delta_s=S_5-S_4\Leftrightarrow5,9=5+\dfrac{\left(5^2-4^2\right)a}{2}\Rightarrow a=\left(0,2m/s^2\right)\)

a)
Chọn chiều (+) hướng lên. Gốc thời gian lúc bắt đầu ném
\(y=v_0t+\frac{gt2}{2}=20t-5t^2\) (1)
\(v=v_0+gt=20-10t\) (2)
Tại điểm cao nhất v=0
Từ (2) \(\Rightarrow\) t=2(s) thay vào (1)
yM = 20(m)
b)
Khi chạm đất y=0 từ (1)\(\Rightarrow\) t=0 và t=4 (s)
Thay t = 4 (s) vào (2) \(v'=-20m\text{/}s\)
(Dấu trừ (-) vận tốc ngược với chiều dương.)

A O x
1) Chọn trục tọa độ Ox như hình vẽ, mốc thời gian lúc ô tô xuất phát.
- Phương trình vận tốc: \(v=v_0+a.t\)
Ban đầu, \(v_0=0\); \(a=0,5m/s^2\)
Suy ra: \(v_1=0,5.t(m/s)\)
- Phương trình tọa độ: \(x=x_0+v_0.t+\dfrac{1}{2}a.t^2\)
\(x_0=0\); \(v_0=0\); \(a=0,5(m/s^2)\)
Suy ra: \(x_1=\dfrac{1}{2}.0,5.t^2=0,25.t^2(m)\)
2) Đổi \(v_{02}=18km/h=5m/s\)
a) Phương trình chuyển động của tàu điện là:
\(x_2=x_0+v_0.t+\dfrac{1}{2}a.t^2=0+5.t+\dfrac{1}{2}.0,3.t^2\)
\(\Rightarrow x_2=5.t+0,15.t^2(m)\)
Ô tôt đuổi kịp tàu điện khi: \(x_1=x_2\)
\(\Rightarrow 0,25.t^2=5.t+0,15.t^2\)
\(\Rightarrow t = 50(s)\)
Vị trí gặp nhau là: \(x=0,25.50^2=625(m)\)
b) Thay \(t=50s\) vào phương trình vận tốc của ô tô và tàu điện ta được:
Vận tốc của ô tô: \(v_1=0,5.t=0,5.50=25(m/s)\)
Vận tốc của tàu điện: \(v_2=5+0,3.t=5+0,3.50=20(m/s)\)

a) PT x1 có dạng tổng quát là: \(x=x_0+v_0t+\dfrac{1}{2}at^2\) nên chuyển động của vật 1 là chuyển động thẳng biến đổi đều.
Căn cứ theo phương trình ta có:
+ \(x_0=0\)
+ \(v_0=-8(m/s)\)
+ \(a=2(m/s^2)\)
Do \(v_0<0\) nên t = 0 thì vật chuyển động ngược chiều dương của trục toạ độ.
Do \(v_0\) ngược dấu với \(a\) nên chuyển động đang là chuyển động chậm dần đều.
PT x2 có dạng tổng quát: \(x=x_0+v.t\) nên chuyển động của vật 1 là chuyển động thẳng đều, căn cứ theo phương trình ta suy ra được:
+ \(x_{02}=12(m)\)
+ \(v_2=5(m/s)\)
Do \(v_2>0\) nên vật 2 đang chuyển động cùng chiều dương với trục toạ độ.
b) Khoảng cách 2 vật là:
\(\Delta x = |x_1-x_2|=|t_2-13t-12|\)
\(t=2(s)\) \(\Rightarrow \Delta x = |2-13.2-12|=36(m)\)
c) Pt vận tốc của vật 2 là:
\(v=v_0+a.t=-8+2.t\) (m/s)
Vật 2 đổi chiều chuyển động khi \(v=0\Rightarrow -8+2.t=0\Rightarrow t = 4(s)\)
Ban đầu, t= 0 thì vị trí vật 2 là: \(x_2=12+5.0=12(m)\)
Khi t = 4s thì vị trí vật 2 là: \(x_2'=12+5.4=32(m)\)
Quãng đường vật 2 đi được là: \(S_2=x_2'-x_2=43-12=20(m)\)
d) Lúc t = 3s, vận tốc vật 1 là: \(v_1=-8+2.3=-2(m/s)\)
Lúc này vật 1 có vận tốc là 2m/s và đang chuyển động chậm dần đều ngược chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
e) Lúc t = 6s, vận tốc vật 1 là: \(v_1=-8+2.6=4(m/s)\)
Lúc này vật 1 có vận tốc là 4m/s và đang chuyển động nhanh dần đều cùng chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
f) Quãng đường vật 1 đi được từ 2s đến 5s là:
\(|(5^2-8.5)-(2^2-8.2)|=3(m)\)