
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



x 4,8 -4,8 O A B C x O A B C 5,5 H1 H2 H
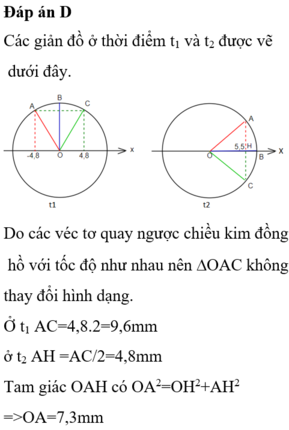
Ta có giản đồ véc tơ ở thời điểm t1 và t2 như hình vẽ.
Do các véc tơ quay ngược chiều kim đồng hồ với tốc độ như nhau nên tam giác AOC không thay đổi hình dạng.
Ở H1: AC = 4,8 . 2 = 9,6 mm.
Ở H2: AH = AC/ 2 = 4,8 mm.
Tam giác AOH có: \(OA^2=\sqrt{OH^2+AH^2}=\sqrt{5,5^2+4,8^2}=7,3\)mm
Vào thời điểm t2, B đang ở biên nên có li độ là 7,3mm.

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Đáp án B

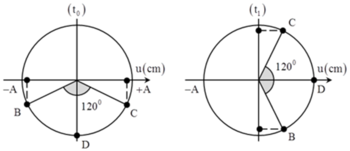
Từ thời điểm t o đến t 1 :
+ Vectơ biểu diễn dao động của B quay góc B: ![]()
+ Vectơ biểu diễn dao động của C quay góc C: ![]()
Ta có: 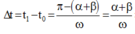
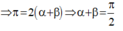
+ Mà: 
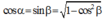

+ Vectơ biểu diễn dao động của D đang từ VTCB cũng quay góc π 2 giống như B và C nên tới vị trí biên.
+ Đến thời điểm t 2 vectơ biểu diễn dao động của D quay thêm góc:


Đáp án C
+ Biểu diễnn các vị trí tương ứng, tại các thời điểm trên đường tròn.
Với góc α luôn không đổi và sin α 2 = v t 1 v m a x = 3 2 ⇒ α = 120 0 .
=> Từ hình vẽ, ta có 3 2 A = 5 3 ⇒ A = 10 m m .

Đáp án A
Có MN = NP. Mặt khác Δ φ M N = 2 π d M N λ ; Δ φ N P = 2 π d N P λ ⇒ Δ φ M N = Δ φ N P . Suy ra trên vòng tròn đơn vị, N luôn là điểm trung tâm của cung MP.
Ta có vòng tròn đơn vị
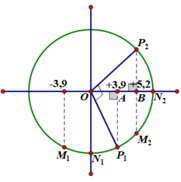
Từ t1 đến t2, điểm N quét 1 góc 90 độ. Vì 3 điểm M, N, P dao động cùng tần số góc, ta suy ra M và P cũng quét 1 góc 90 độ. Suy ra góc P1OP2 = 900. Dễ dàng chứng minh được tam giác P1OA bằng tam giác OP2B (cạnh huyền – góc nhọn), suy ra OA = P2B = 3,9 (cm).
Áp dụng Pytago cho tam giác P2OB, ta có: O P 2 = P 2 B 2 + O B 2 = 6 , 5 ( c m )
Suy ra biên độ dao động A = 6,5 cm. Tại t2, N nằm ở biên (điểm N2 trên hình vẽ) nên li độ của N sẽ là xN = + 6,5 (cm)