Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
câu hỏi của bn có ở đây nhá Câu hỏi của HOC24 - Học và thi online với HOC24
Hệ thức Anh -xtanh trong hiện tượng quang điện
\(hf = A_1+W_{đ1}.(1)\)
\(hf = A_2+W_{đ2}.(2)\)
Ta có \(A_1 = \frac{hc}{\lambda_{01}}; A_2 = \frac{hc}{\lambda_{02}}\)
\( \lambda_{02} = 2\lambda_{01}=> A_1 = 2A_2. \)
Trừ vế với vế của phương trình (1) cho phương trình (2) ta có
=> \(0= A_1-A_2+W_{đ 1}-W_{đ 2}.\)
=> \(W_{đ2}=( A_1-A_2)+W_{đ1} = A_2+W_{đ1}\)
Mà \(A_2 >0\) => \(W_{đ2} > W_{đ1}\).
Giới hạn quang điện là bước sóng lớn nhất chiếu vào kim loại mà gây ra hiệu ứng quang điện phụ thuộc vào bản chất kim loại nên đáp án là B
Vì λ > λ0 
hiện tượng quang điện không xảy ra
Chọn đáp án D.
Đáp án B
Ta có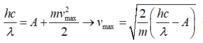 
→ tốc độ lớn nhất thì λ nhỏ nhất.
→ với λ = 0,224 µm
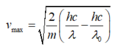
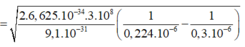
= 0,70.106 m/s.
Động năng ban đầu cực đại của quang electron bứt ra từ mặt quả cầu:
\(\frac{mv^2_{max}}{2}=\frac{hc}{\lambda}-A=2,7.10^{-19}J\)
Gọi Q là điện tích của quả cầu, điện tích này phải là điện tích dương để giữ electron; điện tích Q phân bố đều trên mặt quả cầu, do đó điện thế trên mặt quả cầu là:
\(V=9.10^9.\frac{Q}{R}\). Trên quả cầu hình thành điện trường với các đường sức vuông góc với mặt cầu và hướng ra ngoài ( vì Q>0), điện trường này ngăn cản electron thoát ra khỏi quả cầu, công của điện trường cản là: \(W=eV=9.10^9.\frac{Qe}{R}\)
Muốn cho electron không thoát ra , công đó phải bằng động năng ban đầu cực đại của electron nghĩa là: \(9.10^9.\frac{Qe}{R}=\frac{mv^2_{max}}{2}\)
Thay số ta rút ra : \(Q=1,9.10^{-11}C\)
