Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi No là số photon phát ra trong một đơn vị thời gian, ∈ là năng lượng của mỗi photon, thì
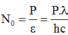
Vì nguồn phát sóng đẳng hướng nên tại điểm cách nguồn một khoảng R, số photon tới là:
![]()
Mà diện tích của con ngươi là:
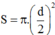
Số photon lọt vào mắt trong một đơn vị thời gian là:

![]()

Số phôtôn phát ra từ nguồn sáng trong 1 s là:
\(N = \frac{P}{\varepsilon} = \frac{P.\lambda}{hc} = \frac{2.0,597.10^{-6}}{6,625.10^{-34}.3.10^8} = 6,01.10^{18} \)(hạt /s); \(P(W)\) là công suất của nguồn sáng, \(\varepsilon\)là năng lượng của phôtôn.
Do nguồn sáng tỏa đều theo mọi hướng => Số phôtôn tới vị trí cách nguồn sáng khoảng cách \(R\) trên 1 đơn vị diện tích, trong 1 đơn vị thời gian là:
\(n = \frac{N}{S_{hình cầu }} = \frac{N}{4\pi R^2} \)
Do con ngươi có đường kính \(d = 4mm\) tương ứng với diện tích \(s_0 = \pi (\frac{d}{2})^2 \). Như vậy số phôtôn lọt vào mắt trong mỗi giây là
\(N_0 = n.s_0 = \frac{N}{4\pi R^2}.\pi (\frac{d}{2})^2 = \frac{N d^2}{16R^2}.\)
Theo bài: \(N_0 \geq 80 => \frac{Nd^2}{16R^2} \geq 80\)
=> \(R \leq \sqrt{\frac{Nd^2}{16.80}} =\frac{d}{4}\sqrt{\frac{N}{80}}=\frac{4.10^{-3}}{4}\sqrt{\frac{6,01.10^{18}}{80}} \approx 274km.\)
Vậy khoảng cách xa nhất từ người quan sát tới nguồn sáng để còn trông thấy nguồn sáng là \(R \approx 274 km.\)

Đáp án D
Gọi No là số photon phát ra trong một đơn vị thời gian, ∈ là năng lượng của mỗi photon, thì
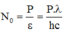
Vì nguồn phát sóng đẳng hướng nên tại điểm cách nguồn một khoảng R, số photon tới là:
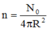
Mà diện tích của con ngươi là:
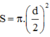
Số photon lọt vào mắt trong một đơn vị thời gian là:
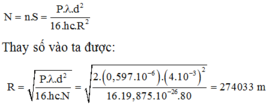

- Gọi N0 là số photon phát ra trong một đơn vị thời gian, ∈ là năng lượng của mỗi photon, thì:

- Vì nguồn phát sóng đẳng hướng nên tại điểm cách nguồn một khoảng R, số photon tới là:

- Mà diện tích của con ngươi là:

- Số photon lọt vào mắt trong một đơn vị thời gian là:

- Thay số vào ta được:




Đáp án: A
Năng lượng mà mắt nhận được trong 1s là:
Mà năng lượng của chùm sáng mắt người nhận được trong 1s là:
W = 80.hc/λ
Suy ra: