Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Q T 4 = ∫ 0 T 4 I 0 sin ω t . d t = − I 0 ω cos ω t π 2 ω 0 = I 0 ω = L C . I 0

Đáp án A
Phương pháp:Sử dụng vecto quay tính thời gian dòng điện chạy qua dây dẫn và công thưc tính điện lượng vàcường độ dòng điện
Cách giải: Cường độ dòng điện trong mạch LC sớm pha π 2 so với điện lượng. Nên khi ban đầu cường độ dòng điện cực đại thì điện lượng bằng 0, cường độ dòng điện đang giảm thì q đang tăng.
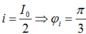
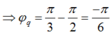
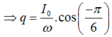


Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng
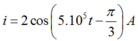
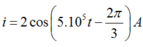
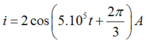
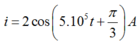
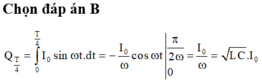
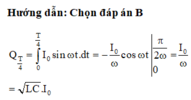
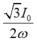
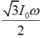
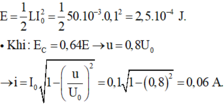
Đáp án A
Phương pháp: Viết phương trình cường độ dòng điện trong mạch.
Cách giải: Giả sử phương trình điện tích là:
Phương trình cường độ dòng điện là: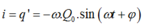
Tụ đang phóng điện tức là q đang giảm, ta có hình vẽ:
Vì q đang giảm nên I đang tăng và ta có phương trình của I là:
Với tần số góc:
Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì năng lượng từ trường cũng bằng một nửa năng lượng từ trường cực đại nên: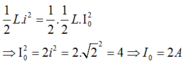
Vậy phương trình của dòng điện I là: