Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)

F 1 = k( l 1 – l 0 )
F 2 = k( l 2 – l 0 )
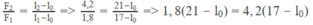
⇒ l 0 = 14(cm)
k = F 1 /( l 1 - l 0 ) = 1,8/3. 10 - 2 = 60(N/m)

1 đầu của lò xo cố định đầu kia kéo bằng lực F
đối với lực kéo F1
\(\Rightarrow F_{đh1}=F_1\Leftrightarrow k.\left(l_1-l_0\right)=F_1\) (1)
đối với lực kéo F2
\(\Rightarrow F_{đh2}=F_2\Leftrightarrow k.\left(l_2-l_0\right)=F_2\) (2)
lấy (1) chia (2)
\(\Leftrightarrow\dfrac{2}{3,6}=\dfrac{l_1-l_0}{l_2-l_0}\Rightarrow l_0=0,13m\)
thay l0 vào (1) koặc (2)
\(\Rightarrow k=40\)N/m

a)Độ lớn của lực đàn hồi: \(F_{đh}=5N\)
b)Độ biến dạng của lò xo: \(\Delta l=\dfrac{F_{đh}}{k}=\dfrac{5}{100}=0,05m=5cm\)
c)Để lò xo dãn thêm 2cm tức \(\Delta l'=2+5=7cm=0,07m\)
Lực đàn hồi lúc này: \(F'_{đh}=0,07\cdot100=7N\)
Cần tăng lực kéo thêm: \(\Delta F=7-5=2N\)
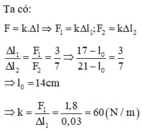


Chọn đáp án C
Ta có: F = k.∆ℓ
→ ℓo = 14 cm