Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
tham khảo
A là biến cố "Hai quả bóng lấy ra đều có màu xanh", \(P\left(A\right)=\dfrac{C^2_5}{C^2_9}\)
B là biến cố "Hai quả bóng lấy ra đều có màu đỏ", \(P\left(B\right)=\dfrac{C^2_4}{C^2_9}\)
\(A\cup B\) là biến cố "Hai bóng lấy ra có cùng màu". A và B xung khắc nên:
\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)=\dfrac{4}{9}\)
\(\Rightarrow C\)
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 13 quả bóng có \({C}_{13}^3 = 286\) cách.
\( \Rightarrow n\left( \Omega \right) = 286\)
a) Gọi \(A\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu xanh”, \(B\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu đỏ”, \(C\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu vàng”
Vậy \(A \cup B \cup C\) là biến cố “Cả 3 quả bóng lấy ra đều có cùng màu”
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 5 quả bóng xanh có \({C}_5^3 = 10\) cách.
\( \Rightarrow n\left( A \right) = 10 \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega\right)}} = \frac{{10}}{{286}} = \frac{5}{{143}}\)
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 6 quả bóng đỏ có \({C}_6^3 = 20\) cách.
\( \Rightarrow n\left( B \right) = 20 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{20}}{{286}} = \frac{{10}}{{143}}\)
Chọn ngẫu nhiên từ hộp 3 quả bóng trong tổng số 2 quả bóng vàng có 0 cách.
\( \Rightarrow n\left( C \right) = 0 \Rightarrow P\left( C \right) = 0\)
\( \Rightarrow P\left( {A \cup B \cup C} \right) = P\left( A \right) + P\left( B \right) + P\left( C \right) = \frac{{15}}{{243}}\)
b) Gọi \(D\) là biến cố “Có đúng 2 quả bóng xanh trong 3 quả bóng lấy ra”
Vậy \(A \cup D\) là biến cố “Có ít nhất 2 quả bóng xanh trong 3 quả bóng lấy ra”
Chọn ngẫu nhiên từ hộp 2 quả bóng trong tổng số 5 quả bóng xanh có \({C}_5^2 = 10\) cách.
Chọn ngẫu nhiên từ hộp 1 quả bóng trong tổng số 8 quả bóng đỏ hoặc vàng có \({C}_8^1 = 8\) cách.
\( \Rightarrow n\left( D \right) = 10.8 = 80 \Rightarrow P\left( D \right) = \frac{{n\left( D \right)}}{{n\left( \Omega \right)}} = \frac{{80}}{{286}} = \frac{{40}}{{143}} \Rightarrow P\left( {A \cup D} \right) = P\left( A \right) + P\left( D \right) = \frac{{45}}{{143}}\)
tham khảo
a) \(A_1\) là biến cố cả 4 quả bóng lấy ra đều có màu xanh; \(P\left(A_1\right)=\dfrac{C^4_5}{C^4_{15}}\)
\(A_2\) là biến cố cả 4 quả bóng lấy ra đều có màu đỏ; \(P\left(A_2\right)=\dfrac{C^4_6}{C^4_{15}}\)
\(A_3\) là biến cố cả 4 quả bóng lấy ra đều có màu vàng; \(P\left(A_3\right)=\dfrac{C^4_4}{C^4_{15}}\)
Khi đó:\(A=A_1\cup A_2\cup A_3\)
Mà \(A_1,A_2,A_3\) là các biến cố xung khắc nên\(P\left(A\right)=P\left(A_1\right)+P\left(A_2\right)+P\left(A_3\right)=\dfrac{1}{65}\)
b) \(B_1\) là biến cố có 2 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; \(P\left(B_1\right)=\dfrac{C^2_5.C^1_6.C^1_4}{C^4_{15}}\)
\(B_2\) là biến cố có 1 quả bóng xanh, 2 quả bóng đỏ, 1 quả bóng vàng; \(P\left(B_2\right)=\dfrac{C^1_5.C^2_6.C^1_4}{C^4_{15}}\)
\(B_3\) là biến cố có 1 quả bóng xanh, 1 quả bóng đỏ, 2 quả bóng vàng; \(P\left(B_3\right)=\dfrac{C^1_5.C^1_6.C^2_4}{C^4_{15}}\)
Khi đó:\(B=B_1\cup B_2\cup B_3\)
Mà \(B_1,B_2,B_3\) là các biến cố xung khắc nên
\(P\left(B\right)=P\left(B_1\right)+P\left(B_2\right)+P\left(B_3\right)=\dfrac{48}{91}\)
a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =
= 3(-1) +2 = -1.
= (-1)2 – 1 = 0.
Vì 
nên không tồn tại 
. Vậy hàm số gián đoạn tại
x0 = -1.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) D = (10.58, -5.6) D = (10.58, -5.6) D = (10.58, -5.6)
đầu tiên giải quyết chia hết cho 2:
lẻ X chẳn
chẳng X chẳn
chẳn X lẻ
(do lấy từ 2 hộp nên dổi vị trí chẳng lẻ cũng được những trường hợp khác nhau)
h giải quyết chie hết cho 3
tích 2 số sẽ chia hết cho 3 nếu một trong 2 số chia hết cho 3 (cái này tự nghiệm 0 chắc đúng)
từ 1=>20 có [3,6,9,12,15,18] là các số chia hết cho 3 ,có 3 chẳng , 3 lẻ
________________________________________________________________
gộp 2 điều kiện
a) lẻ X chẳn
th1: lẻ chia hết cho 3 và chẳn là số bất kì
số trường hợp là : 3 * 10 =30 (vì từ 1=>20 có 10 số chẳn)
th2: lẻ là số bất kì , chẳn chia hết cho 3
cũng như trên 30 cách
b) chẳn X lẻ nói như trên có điều thay dổi vị trí vài chổ
=> cả 2 trường hợp a) b) có 120 cách
c) chẳn X chẳn
lười ghi ...
tư duy như trên nấu cậu có theo giỏi câu trả lời thì bảo tôi tôi giải thích cho
có 60 cách
=> tổng số cách là 120+60=.......180 cách
\(n\left(\Omega\right)=C^3_{30}=4060\)
n(A)\(C^1_{15}\cdot C^2_{15}=1575\)
=>P=1575/4060=45/116
Trong hộp có 30 quả với 15 quả ghi số chẵn, 10 quả mầu đỏ, 5 quả mầu đỏ ghi số chẵn, 25 quả mầu xanh hoặc ghi số lẻ. Vậy theo định nghĩa :
a) \(P\left(A\right)=\dfrac{15}{30}=\dfrac{1}{2}\)
b) \(P\left(B\right)=\dfrac{10}{30}=\dfrac{1}{3}\)
c) \(P\left(C\right)=\dfrac{5}{30}=\dfrac{1}{6}\)
d) \(P\left(D\right)=\dfrac{25}{30}=\dfrac{5}{6}\)
Ta nhận xét rằng khi thả bóng thì bóng đi được 1 lược còn kể từ lần nảy đầu tiên đến khi dừng lại thì bóng đi được 2 lược (1 nảy lên và 1 rơi xuống). Giả sử sau lần nảy thứ n + 1 thì bóng dừng hẳn.
Quãng đường bóng đi được tính đến lần chạm sàn thứ nhất là:
\(S_1=63\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ 2 là:
\(S_2=63+63.\dfrac{1^1}{10^1}\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ (n + 1) là:
\(S_{n+1}=63+63.\left(\dfrac{1}{10}+\dfrac{1}{10^2}+...+\dfrac{1}{10^n}\right)\)
\(=63+63.\dfrac{\dfrac{1}{10}}{1-\dfrac{1}{10}}=70\left(m\right)\)
Vậy độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất là \(70\left(m\right)\)
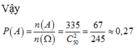
Chọn C
Gọi là biến cố “bốc được quả bóng có tích của số ghi trên quả bóng là một số chia hết cho 10 ”. Xét các tập hợp sau:
Có ba trường hợp xảy ra khi tích của hai số trên hai quả bóng chia hết cho 10.
Trường hợp 1: 1 quả bóng có số ghi thuộc tập B 1 , quả bóng còn lại có số ghi thuộc tập B\ B 1
Khi đó số cách bốc 2 quả bóng là: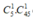
(cách).
Trường hợp 2: 2 quả bóng có số ghi đều thuộc tập B 1 .
Khi đó số cách bốc 2 quả bóng là: C 5 2 (cách).
Trường hợp 3: 1 quả bóng có số ghi thuộc tập B 2 , quả bóng còn lại có số ghi thuộc tập C 2 .
Khi đó số cách bốc 2 quả bóng là:
Suy ra:
Vậy:
=> 0,25 < P < 0,3