Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Khi C=
C
0
,
P
m
a
x
= 60W, khi đó
Z
C
0
=
Z
L
, và ![]()
Khi C= 2 C 0 , thì Z C = 1 / 2 Z C 0 và Pmax =48
=> Z C 0 = R
Khi C=1,5 C 0 , Z C = 2 / 3 Z C 0 => P= 54(W)

Đáp án A
+ Công suất tiêu thụ của mạch khi xảy ra cực đại công suất P = P m a x = 200 W
+ Công suất tiêu thụ của mạch khi xảy ra cực đại của điện áp hiệu dụng trên tụ đi
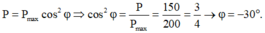
+ Điện áp hai đầu tụ điện
![]()
![]()
=> Công suất tương ứng
![]()
Ghi chú:
Từ công thức:
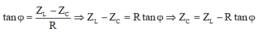
+ Điện áp giữa hai đầu tụ điện
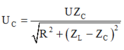
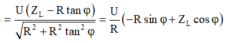
+ Biến đổi lượng giác:
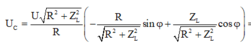
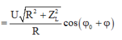

Biểu thức trên trở thành:
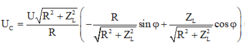
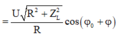
![]()

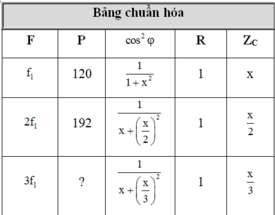
Chuẩn hóa R = 1 Z C = n
Ta có P 2 P 1 = I 2 2 I 1 2 = Z 1 2 Z 2 2 = 1 2 + n 2 1 2 + n 2 2 ⇒ n = 1
Tương tự ta cũng có P 3 = P 1 1 + n 2 1 + n 3 2 = 36 W
Đáp án C

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)
\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)
\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)
Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)
\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)
\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)
\(cos\varphi_2=0,6\)
đáp án B

\(P_1 = P_2 <=> I_1^2R = I_2^2 R\)
<=> \(\frac{U^2}{Z_1^2} R = \frac{U^2}{Z_2^2}R\)
<=> \(Z_1^2 = Z_2^2\)
<=> \(R^2 +(Z_L-Z_{C1})^2 = R^2 +(Z_L-Z_{C2})^2\)
<=> \((Z_L-Z_{C1})^2 =(Z_L-Z_{C2})^2 \)
Mà \(Z_{C1} \neq Z_{C2}\) => \(Z_L - Z_{C1} = -(Z_L-Z_{C2})\)
=> \(Z_L = \frac{Z_{C1}+Z_{C2}}{2} \)
mà công suất của mạch cực đại khi \(Z_L = Z_C => Z_C = \frac{Z_{C_1}+Z_{C_2}}{2}\)
=> \(\frac{1}{C\omega} = \frac{1}{2}(\frac{1}{C_1\omega}+\frac{1}{C_2\omega} )\)
=> \(\frac{1}{C} = \frac{1}{2}(\frac{1}{C_1}+\frac{1}{C_2} ) = \frac{1}{2} (\frac{\pi}{2.10^{-4}}+\frac{3\pi}{2.10^{-4}})\)
=> \(C = \frac{10^{-4}}{\pi} F.\)

em tưởng là P tỉ lệ nghịch với cosφ mà sao bước cuối lại thế kia ạ ?
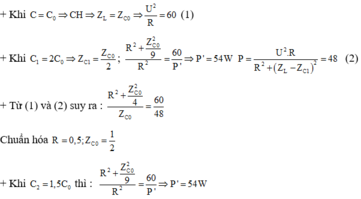
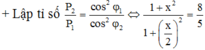
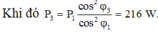
Đáp án B
Khi C=C0 , Pmax= 60W, khi đó Zc0= ZL , và Pmax= U 2 R =60
Khi C= 2C0, thì Zc= ½ ZC0 và Pmax = U 2 R 2 + 1 4 Z C 0 2 R =48
=> ZC0 = R
Khi C=1,5 C0 , ZC= 2/3 ZC0 => P= U 2 R 2 + 2 3 Z C 0 - Z L 2 R = 9U2/10R= 54(W)