Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Đáp án A
Hướng dẫn:
Nhận thấy rằng với cách kích thích bằng va chạm cho con lắc lò xo nằm ngang, chỉ làm thay đổi tần số góc của hệ (do m thay đổi) chứ không làm thay đổi vị trí cân bằng của hệ.
+ Tần số góc của con lắc sau va chạm ω ' = k M + m = 40 0 , 4 + 0 , 1 = 4 5
Tốc độ của vật M khi đi qua vị trí cân bằng v M = ω A = k m A = 50 cm/s.
→ Vận tốc của hệ hai vật sau khi thả nhẹ vật m lên vật M tuân theo định luật bảo toàn độ lượng v 0 = M v M M + m = 40 cm/s
→ Biên độ dao động mới của hệ A ' = x ' 2 + v ' ω ' 2 , trong đó v′ và x′ được xác định ở cùng một thời điểm, do vậy nếu ta chọn thời điểm mà v ′ = v 0 thì x′ = 0 (do hệ M và M đang ở vị trí cân bằng) → A ' = 40 4 5 = 2 5 cm

Giải thích: Đáp án B
Phương pháp: Sử dụng định luật bảo toàn động lượng
Cách giải:
Vận tốc của M khi qua VTCB: 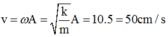
Vận tốc của hai vật khi m dính vào M:![]()
Cơ năng của hệ khi m dính vào M: 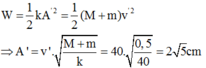

Tần số góc của dao động
+ Tốc độ của vật m khi đi qua vị trí cân bằng
+ Tại vị trí cân bằng vật m’ rơi dính vào vật m. Quá trình này không làm thay đổi vị trí cân bằng của hệ.
Theo phương ngang, động lượng của hệ được bảo toàn → vận tốc của hai vật sau va chạm
Đáp án B