Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Thép có hệ số nở dài nhỏ hơn đồng nên đồng giãn nở nhanh hơn. Mặt khác hai đầu thanh mỗi kim loại bị kẹp chặt nên băng kép sẽ bị cong sao cho chiều dài của đồng lớn hớn chiều dài của thép → băng kép cong lên trên.

Đáp án: D
Thép có hệ số nở dài nhỏ hơn đồng nên đồng giãn nở nhanh hơn. Mặt khác hai đầu thanh mỗi kim loại bị kẹp chặt nên băng kép sẽ bị cong sao cho chiều dài của đồng lớn hớn chiều dài của thép → băng kép cong lên trên.

Gọi:
l01, l02 lần lượt là đường kính của quả cầu thép và của lỗ tròn trên tấm đồng thau ở nhiệt độ 300C
l1, l2lần lượt là đường kính của quả cầu thép và của lỗ tròn trên tấm đồng thau ở nhiệt độ t
α1, α2 lần lượt là hệ số nở dài của thép và đồng thau
+ Ta có: l 1 = l 01 1 + α 1 ∆ t 1 l 2 = l 02 1 + α 2 ∆ t 2
+ Mặt khác, điều kiện để quả cầu lọt qua lỗ tròn: l 1 = l 2 3
Thay (1) và (2) vào (3) ta có: l 01 1 + α 1 ∆ t = l 02 1 + α 2 ∆ t → ∆ t = l 01 - l 02 l 02 α 2 - l 01 α 1 = 0 , 01 . 10 - 3 0 , 06001 . 19 . 10 - 6 - 0 , 06 . 12 . 10 - 6 ≈ 23 , 8 ° C
Nhiệt độ để quả cầu lọt qua lỗ tròn là: t = t 0 + ∆ t = 30 + 23 , 8 = 53 , 8 ° C
Đáp án: C

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l1 – ∆ l2 = l 01 α 1 t – l 02 α 2 t = ( l 01 α 1 – l 02 α 1 )t = 50 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t. Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
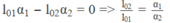
hay:
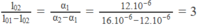
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 3( l 01 - l 02 ) = ∆ l = 3.50 = 150 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 150 + 50 = 200 mm.

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l 1 - l 2 l 1 = l 01 α 1 t - l 02 α 2 t = ( l 01 α 1 - l 02 α 2 )t = 25 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t.
Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
l 01 α 1 - l 02 α 2 = 0 ⇒ l 02 / l 01 = α 1 / α 2
hay:
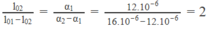
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 2( l 01 - l 02 ) = ∆ l = 2.25 = 50 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 50 + 25 = 75 mm.

Đáp án: D
Gọi l1 là chiều dài của thanh đồng thau, l2 là chiều dài của thanh thép.
Theo giả thiết, ở nhiệt độ bất kỳ ta đều có:
l2 – l1 = 2 cm (1)
Ở 0 oC ta cũng có:
l02 – l01 = 2 cm (2)
Mặt khác, ta lại có:
l2 = l02(1 + α2∆t) và l1 = l01(1 + α1∆t)
Thay l1, l2 vào (1) ta được:
l02(1 + α2∆t) - l01(1 + α1∆t) = l02 – l01
→ l02.α2 = l01.α1 (3)
Từ (2) và (3), chú ý rằng :
α2 = 18.10-6 K-1 và α1 = 11.10-6 K-1
Ta suy ra được chiều dài của thanh thép và thanh đồng ở 0 oC là 5,1cm và 3,1cm

Khi ở nhiệt độ 40oC thì thước thép này dài thêm là: \(\Delta l=\alpha l_0\left(t-t_0\right)=1,2.10^{-5}.0,5.\left(40-0\right)=2,4.10^{-4}m=0,00024m\)
Chiều dài của thước thép ở nhiệt độ 40oC là:
\(0,5+0,00024=0,50024\) m
Chọn đáp án D