Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có công thức xác định vị trí vân trung tâm:
$k_1.\lambda_1=k_2.\lambda_2 =k_3.\lambda_3$
Ta có trong khoảng giữa 2 vân sáng liên tiếp cùng màu với vân trung tâm có 11 vân đỏ thì có 12 khỏang vân ứng với vân đỏ, hay là $k_3 =12$.
Từ đó ta có $k_1=20; k_2 =15$.
Vậy có 14 vân lục và 19 vân tím.
Chọn đáp án C.

Đáp án D
Phương pháp: Vị trí vân trùng nhau: x1 = x2 <=> k1λ1 = k2λ2
Cách giải:
Vị trí trùng nhau của ánh sáng đỏ và lam:
![]()
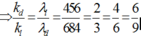
Trong khoảng giữa hai vân sáng có màu cùng màu với vân sáng trung tâm có 6 vân màu lam => kl chạy từ 0 đến 9
Ta có bảng sau:
| kl |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| kd |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
=> Có 3 vân sáng màu đỏ (ứng với k = 1; 3; 5)

Tại vân trung tâm là vân sáng của bước sóng 1 trùng vân sáng của bước sóng 2. Vậy các vân sáng có màu giống vân trung tâm là nơi trùng nhau của vân sáng của bước sóng 1 và vân sáng của bước sóng 2. Vậy ta đi tìm số vị trí trùng nhau.
Ta có: $\frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{{k_2}}}{{{k_1}}} = \frac{3}{2}$
$\Rightarrow {k_1} = 2n$
Các vị trí vân sáng của bước sóng 1 và 2 trùng nhau có tọa độ $x = {k_1}\frac{{{\lambda _1}D}}{a}$ (dùng ${k_2}$ cũng được)
Vì $x \le \frac{L}{2}\Leftrightarrow {k_1}\frac{{{\lambda _1}D}}{a} \le \frac{L}{2}$
$\Leftrightarrow 2n\frac{{{\lambda _1}D}}{a} \le \frac{L}{2}$ (với $n$ là số nguyên dương)
$\Leftrightarrow n = 2$
=>có $2n+1=5$ vị trí trùng nhau.
Đáp số : 5

Đáp án D
Trong các tia thì tia đỏ lệch ít nhất, tia tím lệch nhiều nhất và chiết suất của môi trường đối với ánh sáng đỏ là nhỏ nhất. Nên khi tia màu vàng đi là là trên mặt nước thì các tia có chiết suất lớn hơn sẽ bị phản xạ toàn phần.
Như vậy tia sáng màu đỏ, cam có chiết suất của môi trường đối với các ánh sáng đó nhỏ hơn tia sáng màu vàng nên sẽ ló ra ngoài không khí.

\(Z_{L1}=\omega_1.L=30\) (1)
\(Z_{C1}=\dfrac{1}{\omega_1C}=40\) (2)
Lấy (1) chia (2) vế với vế ta được: \(\omega_1^2LC=\dfrac{3}{4}\) (3)
Khi tần số \(\omega_2\) thì hệ số công suất bằng 1
\(\Rightarrow Z_{L2}=Z_{C2}\Rightarrow \omega_2.L=\dfrac{1}{\omega_2C}\)
\(\Rightarrow \omega_{2}^2LC=1\) (4)
Lấy (4) chia (3) vế với vế \(\Rightarrow \dfrac{\omega_2}{\omega_1}=\dfrac{2}{\sqrt 3}\Rightarrow \omega_2=\dfrac{2}{\sqrt 3}\omega_1\)
Chọn B.

\(\lambda = v.T = \frac{v}{f}=\frac{50}{10}=5cm.\)
Tại M: \(d_{2M}-d_{1M}=18-3=15=3.5\) => M dao động mạnh nhất.
Tại N: \(d_{2N}-d_{1N}=45-10=35=7.5\) => N dao động mạnh nhất.

Đáp án A
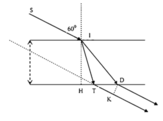
Phương pháp: Định luật khúc xạ ánh sáng n1sini = n2sinr
Cách giải:
Ta có:
![]()
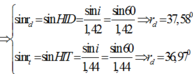
![]()
![]()
Từ hình v có:![]()
=> Bề rộng dải quang phổ liên tục khi chùm sáng ló ra khỏi tấm nhựa:
DK = TD.sinDTK = 0,168.sin30 = 0,084cm

Đáp án B
Phương pháp: Phương trình giao thoa sóng trong giao thoa sóng hai nguồn cùng pha:
u M = 2 acos π ( d 2 - d 1 ) λ cos [ ωt - π ( d 2 + d 1 ) λ ]
Cách giải:
Bước sóng: λ = 2cm
Phương trình sóng tại M:
u M = 2 acos π ( MA - MB ) λ cos [ ωt - π ( MA + MB ) λ ]
X là điểm dao động với biên độ cực đại và ngược pha với M.
Phương trình sóng tại X:
u X = 2 acos π ( XA - XB ) λ cos [ ωt - π ( XA + XB ) λ ]
Vì X và M thuộc elip => M + MB = X + XB
=> uM và uX chỉ khác nhau về:
cos π ( MA - MB ) λ ; cos π ( XA - XB ) λ
Vì M thuộc trung trực của AB
⇒ cos π ( MA - MB ) λ = 1
X ngược pha với M
⇔ cos π ( XA - XB ) λ = - 1 ⇔ X A - X B = ( 2 k + 1 ) λ
- AB ≤ ( 2 k + 1 ) λ ≤ AB ⇔ - 19 ≤ ( 2 k + 1 ) λ ≤ 19 ⇒ - 5 , 25 ≤ k ≤ 4 , 25
=> Có 10 điểm dao động với biên độ cực đại và ngược pha với M trên đoạn B
=> Trên elip có 20 điểm dao động với biên độ cực đại và ngược pha với M.
Đáp án D
Khi chiếu ánh sáng vào các môi trường có chiết xuất khác nhau thì tần số mà màu sắc ánh sáng không đổi
A. Màu cam và tần số 1.5f.
Vì tần số của ánh sáng không thay đổi khi chuyển môi trường, tần số f của ánh sáng trong chất lỏng vẫn là f. Do đó, câu trả lời là: