Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}-\sqrt{ab}=\sqrt{ab}-\sqrt{ab}=0\)
b: \(=\dfrac{\left(\sqrt{x}-2\sqrt{y}\right)^2}{\sqrt{x}-2\sqrt{y}}+\dfrac{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\)
\(=\sqrt{x}-2\sqrt{y}+\sqrt{y}=\sqrt{x}-\sqrt{y}\)
c: \(=\sqrt{x}+2-\dfrac{x-4}{\sqrt{x}-2}\)
\(=\sqrt{x}+2-\sqrt{x}-2=0\)

a, \(\sqrt{75}+\sqrt{48}-\sqrt{300}\)
\(=5\sqrt{3}+4\sqrt{3}-10\sqrt{3}\)
\(=-\sqrt{3}\)
b, \(\sqrt{81a}-\sqrt{36a}+\sqrt{144a}\)
\(=9\sqrt{a}-6\sqrt{a}+12\sqrt{a}\)
\(=15\sqrt{a}\)
c, \(\dfrac{4}{\sqrt{5}-2}-\dfrac{4}{\sqrt{5}+2}\)
\(=\dfrac{4\sqrt{5}+8-4\sqrt{5}+8}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
\(=\dfrac{16}{5-4}=16\)
d, \(\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}=\sqrt{ab}\)
Nguyễn Huy Tú anh sinh năm 2004 là lên lớp 8 mà sao lại tl được bài lớp 9

câu a ở phần mẫu của cụm đầu tiên cái \(\left(\sqrt{a+\sqrt{b}}\right)^2\rightarrow\left(\sqrt{a}+\sqrt{b}\right)^2\) giúp em với ạ ( em cảm ơn )

Ta có : \(a\sqrt{a}-b\sqrt{b}=\left(\sqrt{a}\right)^3-\left(\sqrt{b}\right)^3=\left(\sqrt{a}-\sqrt{b}\right)\cdot\left(a+\sqrt{ab}+b\right)\)Suy ra : a\(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}=a+\sqrt{ab}+b\)
bạn ơi ! bạn giải thích tại sao nó có thể ra đc hằng đẳng thức trên không

\(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{a^3}-\sqrt{b^3}}{\sqrt{a}-\sqrt{b}}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\sqrt{a}-\sqrt{b}}\)
\(=a+\sqrt{ab}+b\)

a, \(\dfrac{b}{\left(a-4\right)^2}.\sqrt{\dfrac{\left(a-4\right)^4}{b^2}}=\dfrac{b}{\left(a-4\right)^2}.\dfrac{\left(a-4\right)^2}{b}=1\)
b, Đặt \(B=\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}\)
\(\sqrt{x}=a,\sqrt{y}=b\)
Ta có: \(B=\dfrac{a^3-b^3}{a-b}=\dfrac{\left(a-b\right)\left(a^2+ab+b^2\right)}{a-b}=a^2+ab+b^2\)
\(\Rightarrow B=x+\sqrt{xy}+y\)
Vậy...
c, \(\dfrac{a}{\left(b-2\right)^2}.\sqrt{\dfrac{\left(b-2\right)^4}{a^2}}=\dfrac{a}{\left(b-2\right)^2}.\dfrac{\left(b-2\right)^2}{a}=1\)
d, \(2x+\dfrac{\sqrt{1-6x+9x^2}}{3x-1}=2x+\dfrac{\sqrt{\left(3x-1\right)^2}}{3x-1}=2x+1\)
a:b(a−4)2.√(a−4)4b2(b>0;a≠4)b(a−4)2.(a−4)4b2(b>0;a≠4)
= \(\dfrac{b}{\left(a-4\right)}.\dfrac{\sqrt{\left[\left(a-4\right)^2\right]^2}}{\sqrt{b^2}}\)
=\(\dfrac{b}{\left(a-4\right)^2}.\dfrac{\left(a-4\right)^2}{b}\)
= 1 ( nhân tử với tử mẫu với mẫu rồi rút gọn)
b:x√x−y√y√x−√y(x≥0;y≥0;x≠0)xx−yyx−y(x≥0;y≥0;x≠0)
=\(\dfrac{\sqrt{x^3}-\sqrt{y^3}}{\sqrt{x}-\sqrt{y}}\)
=\(\dfrac{\left(\sqrt{x}\right)^3-\left(\sqrt{y}\right)^3}{\sqrt{x}-\sqrt{y}}\)
=\(\dfrac{\left(\sqrt{x}-\sqrt{y}\right).\left(x+\sqrt{xy}+y\right)}{\sqrt{x}-\sqrt{y}}\)(áp dụng hằng đẳng thức )
= (x+\(\sqrt{xy}\)+y)
c:a(b−2)2.√(b−2)4a2(a>0;b≠2)a(b−2)2.(b−2)4a2(a>0;b≠2)
Tương tự câu a
d:x(y−3)2.√(y−3)2x2(x>0;y≠3)x(y−3)2.(y−3)2x2(x>0;y≠3)
tương tự câu a
e:2x +√1−6x+9x23x−1
= \(2x+\dfrac{\sqrt{\left(3x\right)^2-6x+1}}{3x-1}\)
= 2x+\(\dfrac{\sqrt{\left(3x-1\right)^2}}{3x-1}\)(hằng đẳng thức)
=2x+\(\dfrac{3x-1}{3x-1}\)
=2x+1

a: \(=x-\sqrt{xy}+y-x+2\sqrt{xy}-y=\sqrt{xy}\)
b: \(=\dfrac{1+\sqrt{a}}{a-\sqrt{a}}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)

Bài 1:
a: ĐKXĐ: 2x+3>=0 và x-3>0
=>x>3
b: ĐKXĐ:(2x+3)/(x-3)>=0
=>x>3 hoặc x<-3/2
c: ĐKXĐ: x+2<0
hay x<-2
d: ĐKXĐ: -x>=0 và x+3<>0
=>x<=0 và x<>-3

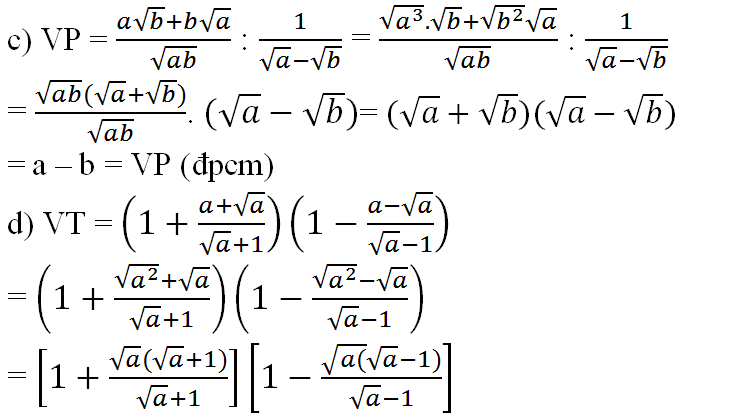
Đề bài là rút gọn hả bn?
Ta có : \(\left(\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}+\sqrt{ab}\right)\)\(\left(\dfrac{\sqrt{a}+\sqrt{b}}{a-b}\right)^2\)=1
⇌ \(\left(\dfrac{\sqrt{a}^3+\sqrt{b}^3}{\sqrt{a}+\sqrt{b}}+\sqrt{ab}\right)\)\(\left(\dfrac{\sqrt{a}+\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\right)^2\)=1
⇌ \(\left(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}+\sqrt{ab}\right)\)\(\dfrac{1}{\left(\sqrt{a}-\sqrt{b}\right)^2}\)=1
⇌ \(\left(a+b\right)\)\(\dfrac{1}{\left(\sqrt{a}-\sqrt{b}\right)^2}\)=1
⇌ \(\dfrac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}-1=0\)
⇌ \(\dfrac{a+b-a+\sqrt{ab}-b}{\left(\sqrt{a}-\sqrt{b}\right)^2}=0\)
⇌ \(\sqrt{ab}=0\)
⇌\(\left[{}\begin{matrix}a=0\\b=0\end{matrix}\right.\)(thỏa mãn điều kiện)
Vậy a=0;b=0