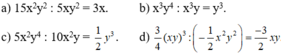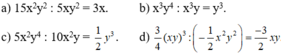
a)
15
x...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. a: \(=\dfrac{4a^2-3a+5}{\left(a-1\right)\left(a^2+a+1\right)}+\dfrac{\left(2a-1\right)\left(a-1\right)}{\left(a-1\right)\left(a^2+a+1\right)}-\dfrac{6a^2+6a+1}{\left(a-1\right)\left(a^2+a+1\right)}\) \(=\dfrac{4a^2-3a+5+2a^2-3a+1-6a^2-6a-6}{\left(a-1\right)\left(a^2+a+1\right)}\) \(=\dfrac{-12a}{\left(a-1\right)\left(a^2+a+1\right)}\) b: \(=\dfrac{5}{a+1}+\dfrac{10}{a^2-a+1}-\dfrac{15}{\left(a+1\right)\left(a^2-a+1\right)}\) \(=\dfrac{5a^2-5a+5+10a+10-15}{\left(a+1\right)\left(a^2-a+1\right)}\) \(=\dfrac{5a^2+5a}{\left(a+1\right)\left(a^2-a+1\right)}=\dfrac{5a}{a^2-a+1}\) a) \(x^2+y^2=\left(x+y\right)^2-2xy=5^2-2.4=25-8=17\) b) \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=5^3-3.4.5=125-60=65\) c) \(x^4+y^4=\left(x^2\right)^2+\left(y^2\right)^2=\left(x^2+y^2\right)^2-2x^2y^2\) \(=\left(\left(x+y\right)^2-2xy\right)^2-2\left(xy\right)^2=\left(5^2-2.4\right)^2-2.4^2\) \(=\left(25-8\right)^2-2.16=17^2-32=289-32=257\) d) \(x^5+y^5=\left(x+y\right)^5-\left(5x^4y+10x^3y^2+10x^2y^3+5xy^4\right)\) \(=\left(x+y\right)^5-5xy\left(x^3+2x^2y+2xy^2+y^3\right)\) \(=\left(x+y\right)^5-5xy\left(\left(x^3+y^3\right)+\left(2x^2y+2xy^2\right)\right)\) \(=\left(x+y\right)^5-5xy\left(\left(x+y\right)^3-3xy\left(x+y\right)+\left(2xy\left(x+y\right)\right)\right)\) \(=\left(5\right)^5-5.4\left(\left(\left(5^3-3.4.5\right)+\left(2.4.5\right)\right)\right)\) \(=3125-20\left(125-65+40\right)\) \(=3125-20\left(100\right)=3125-2000=1125\) \(x^2+y^2=\left(x+y\right)^2-2xy=5^2-2\cdot4=25-8=17\\
x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=5^3-3\cdot4\cdot5=125-60=65\\
x^4+y^4
\\
=\left(x+y\right)^4-4xy\left(x^2+y^2\right)-6x^2y^2\\
=5^4-4\cdot4\left[\left(x+y\right)^2-2xy\right]-6\left(xy\right)^2\\
=5^4-4\cdot4\cdot\left(5^2-2\cdot4\right)-6\cdot4^2\\
=625-16\cdot\left(25-8\right)-6\cdot16\\
=625-16\cdot17-96\\
=625-272-96\\
=257\\
x^5+y^5\\
=\left(x+y\right)^5-5xy\left(x^3+y^3\right)-10x^2y^2\left(x+y\right)\\
=5^5-5\cdot4\left[\left(x+y\right)^3-3xy\left(x+y\right)\right]-10\left(xy\right)^2\cdot5\\
=3125-20\left(5^3-3\cdot4\cdot5\right)-10\cdot4^2\cdot5\\
=3125-20\cdot\left(125-60\right)-10\cdot16\cdot5\\
=3125-20\cdot65-800\\
=3125-1300-800\\
=1025\) a: \(=\dfrac{6x+12+4-2x}{30}=\dfrac{4x+16}{30}=\dfrac{2x+8}{15}\) b: \(=\dfrac{18x}{60}+\dfrac{8x-4}{60}+\dfrac{6-3x}{60}\) \(=\dfrac{18x+8x-4+6-3x}{60}=\dfrac{23x+2}{60}\) c: \(=\dfrac{x+1}{2\left(x-1\right)}-\dfrac{x^2+3}{2\left(x-1\right)\left(x+1\right)}\) \(=\dfrac{x^2+2x+1-x^2-3}{2\left(x-1\right)\left(x+1\right)}=\dfrac{2x-2}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x+1}\) d: \(=\dfrac{x}{y\left(x-y\right)}+\dfrac{2x-y}{x\left(y-x\right)}\) \(=\dfrac{x^2-2xy+y^2}{xy\left(x-y\right)}=\dfrac{x-y}{xy}\) e: \(=\dfrac{x^2+2xy+y^2+x^2+y^2}{x+y}=\dfrac{2x^2+2xy+2y^2}{x+y}\) \(1.\) \(a.\) \(\dfrac{8}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{2}{x^2+3}+\dfrac{1}{x+1}\) \(=\dfrac{8}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{2\left(x^2-1\right)}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{1\left(x-1\right)\left(x^2+3\right)}{\left(x^2-1\right)\left(x^2+3\right)}\) \(=\dfrac{8}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{2x^2-2}{\left(x^2+3\right)\left(x^2-1\right)}+\dfrac{x^3-x^2+3x-3}{\left(x^2-1\right)\left(x^2+3\right)}\) \(=\dfrac{8+2x^2-2+x^3-x^2+3x-3}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=\dfrac{x^3+x^2+3x+3}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=\dfrac{x^2\left(x+1\right)+3\left(x+1\right)}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=\dfrac{\left(x^2+3\right)\left(x+1\right)}{\left(x^2+3\right)\left(x^2-1\right)}\) \(=x-1\) \(b.\) \(\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{2y^2}{x^2-y^2}\) \(=\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{2y^2}{\left(x-y\right)\left(x+y\right)}\) \(=\dfrac{\left(x+y\right)^2}{2\left(x^2-y^2\right)}-\dfrac{\left(x-y\right)^2}{2\left(x^2-y^2\right)}+\dfrac{4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{x^2+2xy+y^2}{2\left(x^2-y^2\right)}-\dfrac{x^2-2xy+y^2}{2\left(x^2-y^2\right)}+\dfrac{4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{4xy+4y^2}{2\left(x^2-y^2\right)}\) \(=\dfrac{4y\left(x+y\right)}{2\left(x^2-y^2\right)}\) \(=\dfrac{2y}{\left(x-y\right)}\) Tương tự các câu còn lại Lời giải: \(B=x(x^2+xy+y^2)-y(y^2+xy+y^2)\) \(=(x-y)(x^2+xy+y^2)=x^3-y^3=10^3-(-1)^3=1000-(-1)=1001\) \(C=x^4+10x^3+10x^2+10\) \(=x^4+9x^3+x^3+9x^2+x^2+10\) \(=x^3(x+9)+x^2(x+9)+x^2+10\) \(=(x+9)(x^3+x^2)+x^2+10\) \(=(-9+9)[(-9)^3+(-9)^2]+(-9)^2+10\) \(=0+(-9)^2+10=91\) Thay $x=-1$ vào biểu thức: \(D=x^2(x+y)-xy(x-y)-x(y^2+1)\) \(=(-1)^2(x+y)-(-1)y(x-y)-(-1)(y^2+1)\) \(=x+y+y(x-y)+(y^2+1)\) \(=x+y+xy-y^2+y^2+1=x+y+xy+1\) \(=(x+1)(y+1)=(-1+1)(y+1)=0\) 1,Thực hiện phép tính : a, (x + 2)9 : (x + 2)6 =(x+2)9-6 =(x+2)3 b, (x - y) 4 : (x - 2)3 =(x-y)4-3 =x-y c, ( x2+ 2x + 4)5 : (x2 + 2x + 4) =(x2+2x+4)5-1 =(x2+2x+4)4 d, 2(x2 + 1)3 : 1/3(x2 + 1) =(2÷1/3).[(x2+1)3÷(x2+1)] =6(x2+1)2 e, 5 (x - y)5 : 5/6 (x - y)2 =(5÷5/6).[(x-y)5÷(x-y)2] =6(x-y))3
K
Khách
CM
Cao Minh Tâm
24 tháng 1 2018
Đúng(0)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 5 2022
22 tháng 8 2017
MV
22 tháng 8 2017
21 tháng 10 2022
8 tháng 12 2017
AH
Akai Haruma
Giáo viên
13 tháng 7 2018
29 tháng 10 2017
