Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.

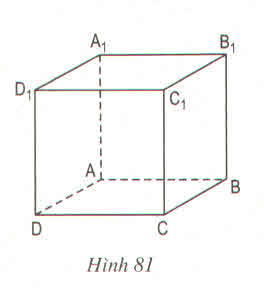
a. Ta có: A1B1 // mp(ABCD)
A1B1 // mp(CDD1C1)
b. Ta có: AC // A1C1
Suy ra: AC không thuộc mp(A1B1C1)

A B C D O K a)Xét tứ giác OBKC, ta có:
OC//BK(BK//AC)
BO//KC(KC//BD)
=>tứ giác OBKC là hình bình hành
lại có:
AC \(\perp\) BD ( hai đường chéo)
BD//KC
=> \(\)góc OCK =90o
=> hình bình hành OBKC là hình chữ nhật
b)Ta có:
BC = OK ( do OCKD là hình chữ nhật)
AB=BC( cách cạnh hình thoi bằng nhau)
=> AB = OK
c)
* nếu tứ giác ABCD là hình vuông:
=>BD=AC
mà: BO=1/2BD
OC=1/2AC
=> BO = OC
=> hình chữ nhật OBKC là hình vuông.
Vậy HCN OBKC là hình vuông khi hình thoi ABCD là hình vuông

) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD

Gt và câu c viết nhầm phải không bạn? Trung tuyến BD,CE,AM chứ. Còn câu b phải qua B kẻ đường thẳng // FD nhỉ? Nếu thế thì lời giải thế này
(lời giải hơi dài tí)
*Xét tứ giác DEMC:
\(ED=\frac{1}{2}BC\)(cma)
\(CM=\frac{1}{2}BC\)(gt)
\(\Rightarrow ED=CM\)
Mà ED//BC (Cma); \(M\in BC\left(gt\right)\)=> ED//CM
Từ 2 chứng minh trên => DEMC là hbh
=>CD//EM(1)
*Mặt khác, ta có: DF//CE(cmb); DF=CE(cmb)
DF//BP(cmc); DF=BP(cmc)
=> CE//BP(cùng //DF); CE=BP(cùng = DF)
Từ chứng minh trên => CEBP là hbh
Nên 2 đường chéo PE và CB cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm CB (gt) => M cũng là trung điểm PE
hay P,M,E thẳng hàng(2)
Từ (1),(2) CD//EP
=> CDEP là hình thang

a: Xét ΔMPQ và ΔNQP có
MQ=NP
\(\widehat{MQP}=\widehat{NPQ}\)
QP chung
Do đó: ΔMPQ=ΔNQP
Suy ra: \(\widehat{IPQ}=\widehat{IQP}\)
=>ΔIQP cân tại I
=>IQ=IP
Ta có: IM+IP=MP
IN+IQ=NQ
mà MP=NQ
và IQ=IP
nên IM=IN
Ta có: \(\widehat{OMN}=\widehat{OQP}\)
\(\widehat{ONM}=\widehat{OPQ}\)
mà \(\widehat{OQP}=\widehat{OPQ}\)
nên \(\widehat{OMN}=\widehat{ONM}\)
hay ΔOMN cân tại O
=>OM=ON
=>O nằm trên đường trung trực của MN(1)
Ta có: IM=IN
nên I nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OI là đường trung trực của MN
b: Ta có: OQ=OP
nên O nằm trên đường trung trực của PQ(3)
Ta có: IQ=IP
nên I nằm trên đường trung trực của PQ(4)
Ta có: KQ=KP
nên K nằm trên đường trung trực của PQ(5)
Từ (3), (4) và (5) suy ra Q,I,K thẳng hàng

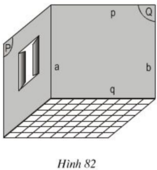

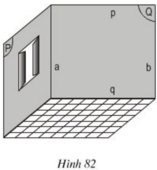


a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.