Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TAM GIÁC ĐỒNG DẠNG
1, a) Tỉ số hai đoạn thẳng AB và AC : \(\frac{AB}{AC}=\frac{6}{15}\)
b) Tỉ số hai đoạn thẳng AB và AC . : \(\frac{AB}{AC}=\frac{6}{18}=\frac{1}{3}\)
2, ΔMNP ~ ΔABC thì : \(\frac{MN}{AB}=\frac{NP}{BC}=\frac{MP}{AC}\)
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm; 10 cm.
4, a) Cho ΔABC có AB=3 cm, AC= 6 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại E. Biết BD= 2cm. Tính độ dài đoạn thẳng EC ❓
Bạn ơi D ở đâu vậy ?
b) Cho ΔABCΔABC có AB = 6 cm, AC= 8 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại D. Biết CD= 4 cm. Tính độ dài đoạn thẳng DB ❓
Xét \(\Delta ABC\) có AD là phân giác
\(\Rightarrow\frac{AB}{BD}=\frac{AC}{CD}\Rightarrow BD=\frac{AB.CD}{AC}=3cm\)
5. a) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k = 2. Tìm tỉ số SDÈFvà SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=2^2=4\)
b) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k=\(\frac{1}{2}\). Tìm tỉ số SDEF và SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
6. Cho ΔABC..Lấy 2 điểm D và E lần lượt nằm trên cạnh AB và AC sao cho AD/AB=AE/AC Kết luận nào sai ❓
A. ΔADE∼ΔABC B. DE//BC
C. AE/AD=AC/AB D. ΔADE=ΔABC
7, Nếu hai tam giác ABC và DEF có góc A= góc D, góc C= góc E thì:
A.ΔABC∼ΔDEF B. ΔABC∼ΔEDF
C. ΔABC∼ΔDFE D.ΔABC∼ΔFED

Bài 1:
TH1: A, D nằm cùng phía với BC
Góc α: Góc giữa C, A, B Góc α: Góc giữa C, A, B Góc β: Góc giữa C, D, B Góc β: Góc giữa C, D, B Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng g: Đoạn thẳng [B, A] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng i: Đoạn thẳng [B, D] Đoạn thẳng j: Đoạn thẳng [D, C] Đoạn thẳng k: Đoạn thẳng [A, D] Đoạn thẳng l: Đoạn thẳng [D, I] Đoạn thẳng m: Đoạn thẳng [A, A'] Đoạn thẳng n: Đoạn thẳng [D, A'] Đoạn thẳng p: Đoạn thẳng [A', C] B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I
Gọi I là trung điểm của BC. Khi đó theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có:
IB = ID = IC
Vậy nên \(\widehat{BDC}=\widehat{BDI}=\frac{\widehat{DIC}}{2}\) (Tính chất góc ngoài) (1)
Trên tia đối của tia IA lấy điểm A' sao cho I là trung điểm AA'.
Tam giác ABC vuông nên ta cũng có IB = IA = IC. Vậy thì IB = IA = IC = IA' hay tam giác ACA' vuông tại C.
Từ đó tương tự như bên trên ta có:
\(\widehat{DAI}=\frac{\widehat{DIA'}}{2};\widehat{CAI}=\frac{\widehat{CIA'}}{2}\)
\(\Rightarrow\widehat{DAC}=\widehat{DAI}-\widehat{CAI}=\frac{\widehat{DIA'}-\widehat{CIA'}}{2}=\frac{\widehat{DIC}}{2}\) (2)
Từ (1) và (2) suy ra \(\widehat{DAC}=\widehat{DBC}\)
Hoàn toàn tương tự ta có: \(\widehat{ADB}=\widehat{ACB}\)
TH2: A, D khác phía với BC
Góc β: Góc giữa C, D, B Góc β: Góc giữa C, D, B Góc γ: Góc giữa B, A, C Góc γ: Góc giữa B, A, C Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng g: Đoạn thẳng [B, A] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng i: Đoạn thẳng [B, D] Đoạn thẳng j: Đoạn thẳng [D, C] Đoạn thẳng k: Đoạn thẳng [A, D] Đoạn thẳng l: Đoạn thẳng [D, I] Đoạn thẳng m: Đoạn thẳng [A, A'] Đoạn thẳng n: Đoạn thẳng [D, A'] Đoạn thẳng p: Đoạn thẳng [A', C] B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) B = (6.06, 3.62) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) C = (8.7, -1.66) Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm I: Trung điểm của f Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm D: Điểm trên c Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I Điểm A': A đối xứng qua I
Tương tự như TH1:
Ta có: \(\widehat{DBC}=\frac{\widehat{DIC}}{2}\)
\(\widehat{DAC}=\widehat{DAA'}+\widehat{A'AC}=\frac{\widehat{DIA'}+\widehat{A'IC}}{2}=\frac{\widehat{DIC}}{2}\)
Vậy nên \(\widehat{DAC}=\widehat{DBC}\)
Tương tự \(\widehat{ADB}=\widehat{ACB}\)
Bài 1:
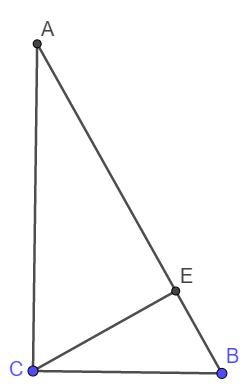
Do BE chia tam giác ABC thành hai tam giác có tỉ số đồng dạng là \(\sqrt{3}\) nên có thể xảy ra các trường hợp sau:
\(\left(1\right)\Delta AEC\sim\Delta EBC;\left(2\right)\Delta AEC\sim\Delta CBE;\left(3\right)\Delta AEC\sim\Delta CEB;\left(4\right)\Delta AEC\sim\Delta ECB\)
(Vì trong các trường hợp còn lại thì tỉ số đồng dạng là \(\frac{EC}{EC}=1\) )
Vì góc \(\widehat{AEC}>\widehat{BCE}\) nên không xảy ta trường hợp (1) và (2); Vì \(\widehat{BEC}>\widehat{EAC}\)nên không xảy ta trường hợp (4)
Do đó chỉ có thể xảy ra trường hợp (3) hay \(\Delta AEC\sim\Delta CEB\Rightarrow\widehat{AEC}=\widehat{BEC}\) và \(\frac{EC}{EB}=\frac{AE}{CE}=\sqrt{3}\)
\(\Rightarrow\widehat{AEC}=\widehat{CEB}=90^o\)
Vậy nên tam giác AEC vuông tại E và \(\frac{AE}{CE}=\sqrt{3}\Rightarrow\widehat{ACE}=60^o;\widehat{CAE}=30^o\)
Vậy tam giác ECB vuông tại E và \(\frac{EC}{EB}=\sqrt{3}\Rightarrow\widehat{CBE}=60^o;\widehat{ECB}=30^o\)
Do đó \(\widehat{CAB}=30^o;\widehat{CBA}=60^o;\widehat{ACB}=90^o.\)

Giải :
a) Xét \(\Delta HBA\)và \(\Delta ABC\)có :
\(\widehat{BHA}=\widehat{BAC}=90^o\)
\(\widehat{B}\)chung
\(\Rightarrow\Delta HBA~\Delta ABC\left(g.g\right)\)
phần B đề sai sửa đề AH2 = HB . HC
Áp dụng hệ thức cạnh trong \(\Delta\)vuông ta có :
\(AH^2=HB.HC\)( đpcm )
chuyên toán thcsLớp 8 chưa học các HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG phải đi c.m chứ

A B C D E 6 H
a) BC = \(\sqrt{AB^2+AC^2}\)= \(\sqrt{6^2+8^2}\)= \(\sqrt{100}\)= 10 (theo định lí Pythagoras)
\(\Delta\)ABC có BD là phân giác => \(\frac{AD}{AB}\)= \(\frac{CD}{BC}\)= \(\frac{AD}{DC}\)= \(\frac{AB}{BC}\)= \(\frac{6}{10}\)= \(\frac{3}{5}\).
b) Ta có : \(\widehat{ABE}\)= \(\widehat{EBC}\)(BD là phân giác)
=> \(\Delta ABD\)~ \(\Delta EBC\)(gg)
=> \(\frac{BD}{BC}\)= \(\frac{AD}{EC}\)<=> BD.EC = AD.BC (đpcm).
c) Ta có : \(\Delta CHE\)~ \(\Delta CEB\)( 2 tam giác vuông có chung góc C )
=> \(\frac{CH}{CE}\)= \(\frac{CE}{CB}\)<=> CH.CB = CE2 (1)
\(\Delta CDE\)~ \(\Delta BDA\)(gg (2 góc đối đỉnh))
\(\Delta BDA~\Delta BCE\) (câu b))
=> \(\Delta CDE~\Delta BCE\)
=> \(\frac{CE}{BE}\)= \(\frac{DE}{CE}\)<=> BE.DE = CE2 (2)
Từ (1) và (2) => CH.CB = ED.EB (đpcm).

a. xét tam giác ABC và AHB có:
góc A chung
góc B= góc H (=90)
suy ra 2 tam giác đồng dạng nên \(\frac{AB}{AH}=\frac{AC}{AB}\Rightarrow AB^2=AH.AC\)
b. Xét tam giác CBH và CAB có:
góc C chung
góc H=góc B (=90)
suy ra 2 tam giác đồng dạng nên \(\frac{BC}{AC}=\frac{HC}{BC}\Rightarrow BC^2=AC.HC\)
c. Áp dụng Pytago cho tam giác ABC => \(AC=\sqrt{AB^2+BC^2}=\sqrt{20^2+15^2}=25\)
theo a suy ra \(AH=\frac{AB^2}{AC}=\frac{400}{25}=16\)
Vì tam giác ABC đồng dạng với tam giác MNP theo tỉ số 2 3 nên
A B M N = A C M P = B C N P = A B + A C + B C M N + M P + N P = P A B C P M N P
và A B M N = 2 7 ⇒ P A B C P M N P = 2 7
Từ đó
P M N P = 7 P A B C 2 = 7.14 2 = 49 c m
Đáp án: D