Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)
Chọn A
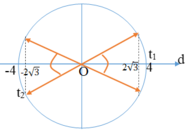
Khoảng cách giữa hai vật theo phương Ox là:
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.
. Khoảng cách lớn nhất giữa hai chất điểm gần giá trị nào nhất sau đây:
Giải thích: Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán khoảng cách giữa hai chất điểm dao động điều hòa
Cách giải:
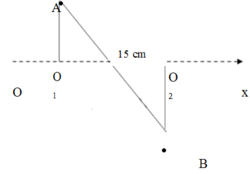
+ Khoảng cách giữa hai chất điểm theo phương thẳng đứng:
+ Khoảng cách lớn nhất giữa hai chất điểm là:
Chọn D
Khoảng cách giữa hai dao động được mô tả bởi phương trình
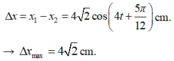
Giải thích: Đáp án D
Phương pháp: Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng tần số kết hợp với bất đẳng thức Bu-nhi-a-cốp-xki để đánh giá
Cách giải:
Giả sử phương trình dao động của M và N lần lượt là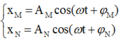 
Biên độ dao động tổng hợp của hai dao động trên là: 
Khoảng cách lớn nhất của M và N trên phương Ox là: 
Theo đề bài ta có: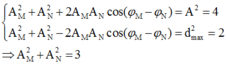 
Thấy rằng: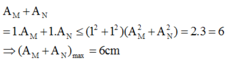 
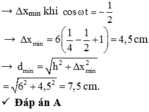
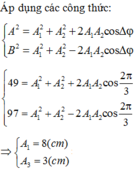
Chọn A.
Khoảng cách giữa hai điểm trong quá trình dao động = Δ = d 2 + 2 2 , với d à khoảng cách trên trục Ox của 2 chất điểm. Ta có: