Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là:
\(\Omega=\left\{\left(i;j\right)\le i;j\le6\right\}\Rightarrow n\left(\Omega\right)=6^2=36\)
a) A là biến cố “Hai con xúc sắc đều xuất hiện mặt chẵn”
Suy ra: A = { (2, 2); (4, 4); ( 6, 6); (2, 4); (4, 2); (2, 6); (6, 2); (4, 6); (6, 4)}
Suy ra: n(A) = 9
Vậy \(P\left(A\right)=\dfrac{9}{36}=\dfrac{1}{4}\)
b) Gọi B là biến cố: “Tích các số chấm trên hai con xúc sắc là số lẻ”.
⇒ B = {(1, 1); (1, 3); (1, 5); (3, 1); (3, 3); (3, 5); (5, 1); (5, 3); (5, 5)}
⇒ n(B) = 9
Vậy \(P\left(B\right)=\dfrac{9}{36}=\dfrac{1}{4}\)

Không gian mẫu là kết quả của việc gieo đồng thời hai con xúc sắc.
⇒ Ω = {(i; j); 1 ≤ i, j ≤ 6}.
⇒ n(Ω) = 6.6 = 36.
a) Gọi A: “Cả hai con xúc sắc đều xuất hiện mặt chẵn”
⇒ A = {(2; 2); (2; 4); (2; 6); (4; 2); (4; 4); (4; 6); (6; 2); (6; 4); (6; 6)}
⇒ n(A) = 9.
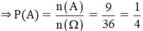
b) Gọi B: “Tích số chấm trên hai con xúc sắc là số lẻ”
Vì tích hai số là lẻ chỉ khi cả hai thừa số đều lẻ nên :
B = {(1; 1); (1; 3); (1; 5); (3; 1); (3; 3); (3; 5); (5; 1); (5; 3); (5; 5)}
⇒ n(B) = 9

Chọn B
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố thỏa mãn yêu cầu bài toán:
![]()
![]() nên n(A) = 8
nên n(A) = 8
Vậy ![]()

Không gian mẫu là Ω = {1, 2, 3, 4, 5, 6}. Số kết quả có thế có thể có là 6 (hữu hạn); các kết quả đồng khả năng.
Ta có bảng:
|
b |
1 |
2 |
3 |
4 |
5 |
6 |
|
∆ = b2 - 8 |
-7 |
-4 |
1 |
8 |
17 |
28 |
a) Phương trình x2 + bx + 2 = 0 có nghiệm khi và chỉ khi ∆ = b2 - 8 ≥ 0 (*). Vì vậy nếu A là biến cố: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 có nghiệm"
thì A = {3, 4, 5, 6}, n(A) = 4 và
P(A) = =
.
b) Biến cố B: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 vô nghiệm" là biến cố A, do đó theo qui tắc cộng xác suất ta có
P(B) = 1 - P(A) = .
c) Nếu C là biến cố: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 có nghiệm nguyên" thì C = {3}, vì vậy
P(C) = .

Đáp án D
Tổng số chấm bẳng 2 khi số chấm ở 2 con xúc sắc là (1; 1).
Tổng số chấm bẳng 3 khi số chấm ở 2 con xúc sắc là (1; 2); (2; 1)
Tổng số chấm bẳng 4 khi số chấm ở 2 con xúc sắc là (1; 3); (2; 2); (3; 1)
Tổng số chấm bẳng 5 khi số chấm ở 2 con xúc sắc là (1; 4), (2; 3), (3; 2); (4; 1)
Do đó xác suất là 10 . 1 36 = 5 18


Đáp án là A.
• Số phần tử không gian mẫu n ( Ω ) = 36
• Gọi biến cố A: " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".
Ta có các khả năng xảy ra: