Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
.
.
.
.
là VTCP của 2 đường thẳng d và d’. Nếu 
thì:
. Khi đó 
bằng:
. Tính 
. Khi đó:
.
. Tìm b.
.
. Tính 
.
và 
. Khi đó:
.
với 
.
và 
. Khi đó 
bằng:
. Khi đó 
bằng:
. Khi đó 
bằng
. Tính 
.
2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42
Chọn B
Số phần tử không gian mẫu là số cách chia 8 đội bóng vào hai bảng sao cho mỗi bảng có 4 đội
Gọi A là biến cố thỏa mãn yêu cầu bài toán.
Ta có: 
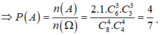
1. Không gian mẫu: \(C_{12}^4C_8^4C_4^4\)
Xếp 3 đội Việt Nam vào 3 bảng: \(3!=6\) cách
Còn 9 đội nước ngoài, có \(C_9^3C_6^3C_3^3\) cách xếp
Xác suất: \(P=\dfrac{6.C_9^3C_6^3C_3^3}{C_{12}^4C_8^4C_4^4}=...\)
2.
Không gian mẫu: \(C_{11}^2\)
Tích 2 số chẵn khi có ít nhất 1 số chẵn
Số cách chọn 2 thẻ đều lẻ: \(C_6^2\)
Số cách chọn ít nhất 1 thẻ chẵn: \(C_{11}^2-C_6^2\)
Xác suất: \(P=\dfrac{C_{11}^2-C_6^2}{C_{11}^2}=...\)
https://hoc24.vn/cau-hoi/bai-1-cho-tam-giac-abc-co-ba-goc-nhon-ke-hai-duong-cao-bd-va-ce-goi-m-n-lan-luot-la-hinh-chieu-cua-bc-tren-duong-thang-de1tu-giac-bmnc-la-hinh-givi-sao2goi-o-la-trung-diem-cua-doan-tha.329689210002 cho e spam xíu ạ , giúp e với
Chọn D
Nhận định bài toán:
1) Đây là dạng bài toán phân chia một tập hợp ra thành các nhóm có số lượng bằng nhau.
2) Phương pháp:
Dạng bài toán này được phân chia làm 2 loại đó là:
- Các nhóm có thứ tự A, B, C, D…
- Các nhóm không phân biệt thứ tự.
Nếu không phân biệt rõ ràng 2 bài toán này thì rất dễ dẫn đến nhầm lẫn và sai kết quả.
Ví dụ: Có bao nhiêu cách chia 20 người thành 4 nhóm, mỗi nhóm có 5 người trong các trường hợp sau:
a) Các nhóm được đánh tên theo thứ tự A, B, C, D.
b) Không phân biệt thứ tự nhóm.
Lời giải
a) Số cách chọn 5 người cho nhóm A là C 20 5 . Ứng với mỗi cách chọn trên, ta có số cách chọn 5 người cho nhóm B là C 15 5 , nhóm C là C 10 5 và 5 người còn lại vào nhóm D.
Theo quy tắc nhân, ta được số cách chia nhóm là: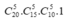 
(cách).
b) Vì các nhóm không phân biệt thứ tự nên khi ta hoán vị 4 nhóm trên sẽ cho cùng một kết quả. Do đó số cách chia trong trường hợp này là
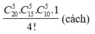
3) Phân tích bài toán và lời giải.
Chia 8 đội thành hai bảng đấu, do đó hai bảng đấu này sẽ có thứ tự rõ ràng cho nên bài toán của chúng ta thuộc loại chia nhóm có thứ tự.
Gọi hai bảng đấu là bảng A và bảng B.
Chọn 4 đội vào bảng A ta có C 8 4 cách, bốn đội còn lại vào bảng B có 1 cách.
Theo quy tắc nhân, ta có số cách chia 8 đội vào hai bảng đấu là:
Gọi A là biến cố “Hai đội Việt Nam nằm ở hai bảng khác nhau”.
Bảng A: Có 3 đội nước ngoài và 1 đội Việt Nam. Số cách chọn là C 6 3 . C 2 1 .
Bảng B: Chỉ còn 1 cách chọn duy nhất cho 3 đội nước ngoài và 1 đội Việt Nam còn lại vào bảng B.
Do đó số cách chia 8 đội thành 2 bảng mỗi bảng có 1 đội Việt Nam là : n(A) = C 6 3 . C 2 1 .1 = 40 cách
Vậy xác suất của biến cố A là: 
Đáp án B
Số cách sắp ngẫu nhiên là C 9 3 . C 6 3 . C 3 3 = 1680 (cách).
Số cách sắp để ba đội của Việt Nam ở 3 bảng khác nhau là
( C 6 2 C 3 1 ) ( C 4 2 C 2 1 ) ( C 2 2 C 2 1 ) = 540 cách.
Xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: 540 1680 = 9 28 .
Đáp án C
Cách chia 9 đội ra thành 3 bảng là
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là
⇒ p = 540 1680 = 9 28
Đáp án: D.
Số phần tử của không gian mẫu là: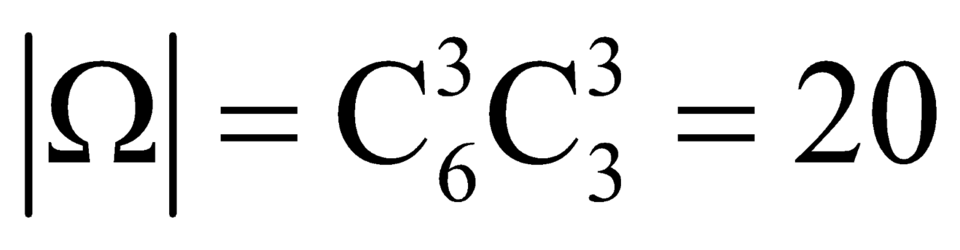
.
Gọi A là biến cố: “đội tuyển U21 HA.GL và U21 Thái Lan nằm ở hai bảng khác nhau”. Số kết quả thuận lợi cho biến cố A là:
Vậy xác suất cần tính là