Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn giải:
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)

Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: 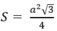
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: 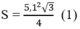
Diện tích hình quạt tròn AOB là:
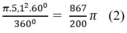
Từ (1) và (2) suy ra diện tích hình viên phân là:
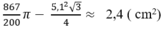
Kiến thức áp dụng
+ Diện tích tam giác đều cạnh a là:
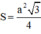
+ Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
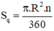

góc AOB=180-60=120 độ
S OAB=1/2*OA*OB*sinAOB=\(R^2\cdot\dfrac{\sqrt{3}}{4}\)
S q OAB=\(pi\cdot R^2\cdot\dfrac{120}{360}=pi\cdot R^2\cdot\dfrac{1}{3}\)
=>\(Svp=R^2\left(pi\cdot\dfrac{1}{3}-\dfrac{\sqrt{3}}{4}\right)\)

A B C D E x y
a) Xét tứ giác BEDC có:
\(\widehat{BEC}=\widehat{BDC}\)
\(\widehat{BEC}\)và \(\widehat{BDC}\) cùng nhìn cạnh BC
=> BEDC là tứ giác nội tiếp
b) Do BEDC là tứ giác nội tiếp nên: \(\widehat{BED}+\widehat{BCD}=180^o\)
Mà \(\widehat{BED}+\widehat{DEA}=180^o\Rightarrow\widehat{BCD}=\widehat{DEA}\)(*)
Mặt khác ta có:
\(\widehat{xAB}=\widehat{ACB}\)(cùng chắn cung AB)
hay \(\widehat{xAE}=\widehat{BCD}\)(**)
Từ (*) và (**) suy ra \(\widehat{DEA}=\widehat{xAE}\)
=> xy song song với ED (2 góc sole trong) (đpcm)
c) Do tứ giác BEDC là tứ giác nội tiếp
Mà \(\widehat{EBD}\)và \(\widehat{ECD}\)cùng nhìn cạnh ED
=> \(\widehat{EBD}=\widehat{ECD}\)(đpcm)
d) \(\widehat{BOC}=2\widehat{BAC}=120^o\)
DIện tích hình quạt BOC là: \(S_{qBOC}=\frac{\pi.R.n}{180}=\frac{\pi.2.120}{180}=\frac{4}{3}\pi\left(cm^2\right)\)
\(BC^2=OB^2+OC^2-2.OB.OC.cos120^o=12\Rightarrow BC=2\sqrt{3}\)
OH là đường cao, tam giác BOC cân tại O => BH=1/2.BC=\(\sqrt{3}\left(cm\right)\)
\(OH^2=OB^2-BH^2=2^2-3=1\Rightarrow OH=1\left(cm\right)\)
Diện tích tam giác BOC là: \(S_{\Delta BOC}=\frac{1}{2}.OH.BC=\frac{1}{2}.1.2\sqrt{3}=\sqrt{3}\left(cm^2\right)\)
=> Diện tích hình viên phân là: \(S_{vp}=S_{qBOC}-S_{\Delta BOC}=\frac{4}{3}\pi-\sqrt{3}\left(cm^2\right)\)
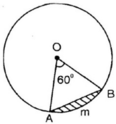
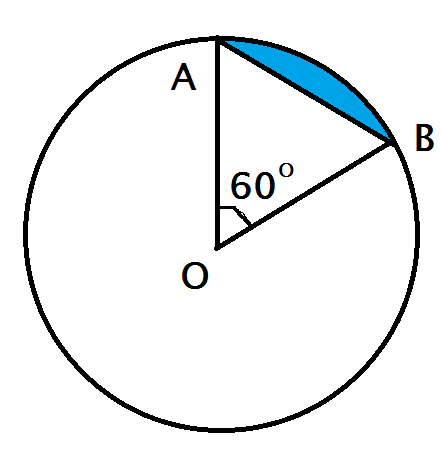
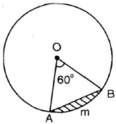


Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: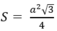
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: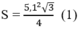
Diện tích hình quạt tròn AOB là:
Từ (1) và (2) suy ra diện tích hình viên phân là: