Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

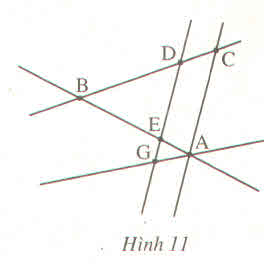
a) Các bộ ba điểm thẳng hàng là: (A, E, B); (B, D, C); (D, E, G).
b) Hai bộ ba điểm không thẳng hàng là: (A, C, B); (A, G, D).
Với câu này có khá nhiều đáp án. Các bạn nhìn hình vẽ và chỉ ra hai bộ ba điểm không thẳng hàng bất kì. Ví dụ như: (A, E, G); (A, D, C); (D, E, C); ...

Trước hết ta cần nhận xét:
\(\left(-1\right)+\left(-2\right)+\left(-3\right)+\left(-4\right)+5+6+7=8\)
Mặt khác, tổng của ba bộ số "thẳng hàng" bằng 0 nên ta có tổng của sáu số xung quanh và ba số đứng giũa cũng bằng 0.
Từ đó suy ra: Số đứng giữa + số đứng giữa +8 = 0, nên số đứng giữa = -4.
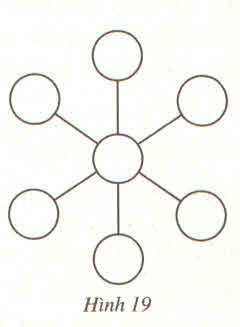
Từ đó, ta có cách điền như hình 19 dưới đây
-4 -3 -2 -1 7 6 5 Hình 19
Trước hết ta cần nhận xét:
\(\left(1\right)+\left(-2\right)+-3+\left(-4\right)+5+6+7=8\)
Mặt khác, tổng của ba bộ số "thẳng hàng" bằng 0 nên ta có tổng của sáu số xung quanh và ba số đứng giũa cũng bằng 0.
Từ đó suy ra: Số đứng giữa + số đứng giữa +8 = 0, nên số đứng giữa = -4.
Từ đó, ta có cách điền như hình 19 dưới đây
7 6 5 -4 -3 -2 -1 Hình 19

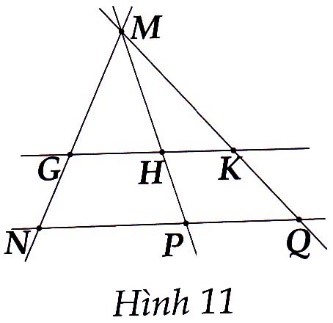
a) Có tất cả năm bộ ba điểm thẳng hàng:
N, G, M; M, H, P; M, K, Q; G, H, K; N, P, Q
b) Hai bộ ba điểm không thẳng hàng:
M, G, P; H, K, P

Ta có : \(\overline{abcdeg}=\overline{ab}.1000+\overline{cd}.100+\overline{eg}\)
\(=9999.\overline{ab}+\overline{ab}+99.\overline{cd}+\overline{cd}+\overline{eg}\)
\(=\left(9999.\overline{ab}+99.\overline{cd}\right)+\left(\overline{ab}+\overline{cd}+\overline{eg}\right)\)
Vì : \(9999.\overline{ab}+99.\overline{cd}⋮11\) và \(\overline{ab}+\overline{cd}+\overline{eg}⋮11\)
\(\Rightarrow\overline{abcdeg}⋮11\left(đpcm\right)\)
Ta có:
\(\overline{abcdeg}=\overline{ab}.10000+\overline{cd}.100+\overline{eg}\)
\(=\overline{ab}.9999+\overline{ab}+\overline{cd}.99+\overline{cd}+\overline{eg}\)
\(=\overline{ab}.11.909+\overline{cd}.11.9+\left(\overline{ab}+\overline{cd}+\overline{eg}\right)\)
\(=11\left(\overline{ab}.909+\overline{cd}.9\right)+\left(\overline{ab}+\overline{cd}+\overline{eg}\right)\)
Vì \(11\left(\overline{ab}.909+\overline{cd}.9\right)⋮11\) và \(\overline{ab}+\overline{cd}+\overline{eg}⋮11\)
nên \(\overline{abcdeg}⋮11\)
Vậy nếu \(\overline{ab}+\overline{cd}+\overline{eg}⋮11\) thì \(\overline{abcdeg}⋮11\) (đpcm)
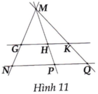

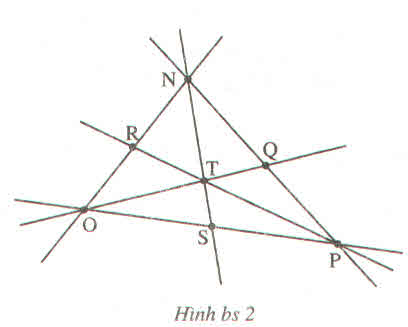
Hai bộ ba điểm không thẳng hàng:
M, G, P
N, H, K