Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

Đáp án B

ZC= 90, R=90 => u A M chậm pha π/4 so với i
u A M chậm pha π/2 so vơi u M B nên u M B nhanh pha hơn i π/4
=> MB chứa 2 thành phần R 0 và L
![]()
![]() mH
mH

Đáp án B
Nhìn vào đồ thị dễ dàng tìm được 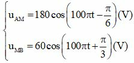
Giản đồ :
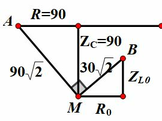
Từ giản đồ suy ra được R 0 = Z L 0 = 30 Ω => R 0 = 30Ω ; L 0 = 95,5 mH.

Lúc sau: \(P'=\frac{U^2.R^2}{R^2_2+Z^2_C}=\frac{U^2.R^2}{R^2_2+R_1R_2}=\frac{U^2}{R_1+R_2}=P=85W\)

Đáp án: B
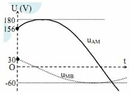
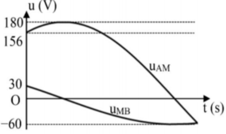
Từ đồ thị ta thấy U0AM = 180 V; U0MB = 60 V.
Tại t = 0, u A M = 90 3 V và đang tăng
→ 90 3 = 180 cos φ 1 , φ1 < 0 → φ1 = -π/6
Tại t = 0 uMB = 30 V và đang giảm 30 = 60 cos φ 2 , φ2 > 0 → φ2 = π/3
Suy ra uAM và uMB vuông pha với nhau => hộp X chứa R0 và L0
ZC = 90 W.
Ta có
R 0 2 + Z L 2 R 2 + Z 2 = U 0 M B U 0 A M 2 = 1 9 → R 0 2 + Z L 2 = 1800
=> chỉ có đáp án B phù hợp.

Đáp án: B.
Từ đồ thị ta thấy U0AM = 180 V; U0MB = 60 V.
Tại t = 0, uAM = 90√3 V và đang tăng
→ 90√3 = 180cosφ1, φ1 < 0 → φ1 = -π/6
Tại t = 0 uMB = 30 V và đang giảm 30 = 60 cosφ2, φ2 > 0 → φ2 = π/3
Suy ra uAM và uMB vuông pha với nhau => hộp X chứa R0 và L0
ZC = 90 W.
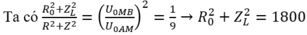
=> chỉ có đáp án B phù hợp.
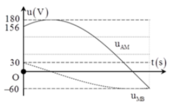



Đáp án B
Tại thời điểm t = 0, xét tỉ số
điện áp tức thời trên đoạn mạch MB sớm pha 0 , 5 π so với điện áp tức thời trên đoạn AM
+ Điều này chỉ xảy ra khi X chứa hai phần tử là R 0 và L 0 . Ta có
Vậy tan φ M B = 1 ⇒ R 0 = Z L
Mặc khác