
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vậy:
Khi bán kính tăng lên gấp đôi thì diện tích đường tròn tăng lên gấp 4 (= 22) lần.
Khi bán kính tăng lên gấp ba thì diện tích đường tròn tăng lên gấp 9 (= 32) lần.
Khi bán kính tăng lên gấp k thì diện tích đường tròn tăng lên gấp k2lần.
Kiến thức áp dụng
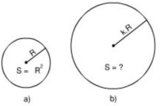
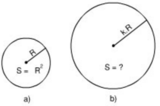
+ Diện tích hình tròn bán kính R là: S = πR2.

Ta có:
π(2R)2 = 4πR2
π(3R)2 = 9 πR2
π(kR)2 = k2 πR2
Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với k > 0 thì diện tích hình tròn sẽ gấp k2 lần
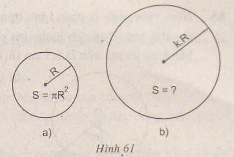
Ta có:
π(2R)2 = 4πR2
π(3R)2 = 9 πR2
π(kR)2 = k2 πR2
Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với k > 0 thì diện tích hình tròn sẽ gấp k2 lần.

Gọi S = π R 2 là diện tích hình tròn lúc đầu
Khi bán kính tăng gấp ba, tức là R 2 = 3 R
![]()

Khi bán kính tăng gấp k lần (k>1) tức là
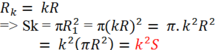
Vậy:
Khi bán kính tăng lên gấp đôi thì diện tích đường tròn tăng lên gấp 4 (= 22) lần.
Khi bán kính tăng lên gấp ba thì diện tích đường tròn tăng lên gấp 9 (= 32) lần.
Khi bán kính tăng lên gấp k thì diện tích đường tròn tăng lên gấp k2lần.

Hướng dẫn giải:
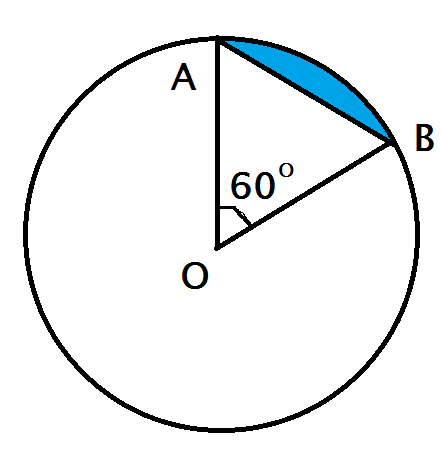
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)

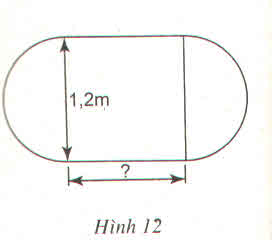
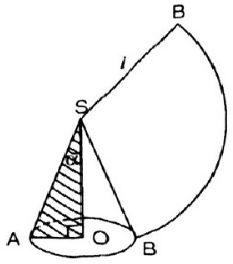
Giải:
Diện tích hình quạt :
Diện tích xung quanh của hình nón: Sxq = π.r.l
Theo đầu bài ta có: Sxq= Sq => π.r.l=
Vậy l = 4r
Suy ra sin(a) = = 0,25
Vậy a = 14o28’

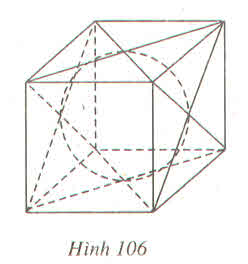
Ta thấy ngay cạnh của hình lập phương gấp đôi bán kính hình cầu
a) Tỉ số cần tính \(\dfrac{6}{\pi}\)
b) Diện tích toàn phần của hình lập phương là \(42cm^2\)
c) Thể tích cần tính xấp xỉ \(244cm^3\)
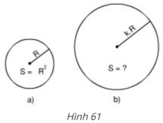
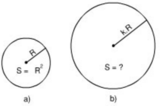

Gọi S = S = π R 2 là diện tích hình tròn lúc đầu
Khi bán kính tăng gấp đôi, tức là R 1 = 2 R