
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

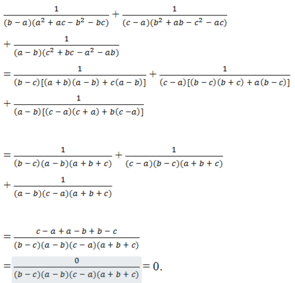

áp dụng BĐT cô si dạng engel cho 3 số dương, ta có:
\(\dfrac{\left(2b+3c\right)^2}{a}+\dfrac{\left(2c+3a\right)^2}{b}+\dfrac{\left(2a+3b\right)^2}{c}\ge\dfrac{\left(5a+5b+5c\right)^2}{a+b+c}=\dfrac{25\left(a+b+c\right)^2}{a+b+c}=25\left(a+b+c\right)\left(đpcm\right)\)

câu 6 :
số hs nữ = 34 hs
số học sinh nam giỏi = hs nữ khá
=> số hs giỏi = số hs giỏi nữ+số học sinh nam giỏi = số hs nữ giỏi + số học sinh nữ khá = số học sinh giỏi cả lớp =34

Ta có:
\(a^2+ac-b^2-bc=\left(a^2-b^2\right)+\left(ac-bc\right)\)
\(=\left(a-b\right)\left(a+b\right)+c\left(a-b\right)\)
\(=\left(a-b\right)\left(a+b+c\right)\)(1)
\(b^2+ab-c^2-ac=\left(b^2-c^2\right)+\left(ab-ac\right)\)
\(=\left(b-c\right)\left(b+c\right)+a\left(b-c\right)\)
\(=\left(b-c\right)\left(a+b+c\right)\)(2)
\(c^2+bc-a^2-ab=\left(c^2-a^2\right)+\left(bc-ab\right)\)
\(=\left(c-a\right)\left(a+c\right)+b\left(c-a\right)\)
\(=\left(c-a\right)\left(a+b+c\right)\)(3)
Ta có : \(\frac{1}{\left(b-c\right)\left(a^2+ac-b^2-bc\right)}\)\(+\frac{1}{\left(c-a\right)\left(b^2+ab-c^2-ac\right)}\)\(+\frac{1}{\left(a-b\right)\left(c^2+bc-a^2-ab\right)}\)(*)
Thế (1),(2),(3) vào (*)
=>\(\frac{1}{\left(b-c\right)\left(a-b\right)\left(a+b+c\right)}+\frac{1}{\left(c-a\right)\left(b-c\right)\left(a+b+c\right)}+\frac{1}{\left(a-b\right)\left(c-a\right)\left(a+b+c\right)}\)
\(\Leftrightarrow\frac{\left(c-a\right)+\left(a-b\right)+\left(b-c\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)}=0\)
Dễ thôi bạn chỉ cần quy đồng thôi
\(\frac{1}{\left(b-c\right)\left(a^2+ac-b^2-bc\right)}+\frac{1}{\left(c-a\right)\left(b^2+ab-c^2-ac\right)}+\)\(\frac{1}{\left(a-b\right)\left(c^2+bc-a^2-ab\right)}\)
=\(\frac{1}{\left(b-c\right)\left(a-b\right)\left(a+b+c\right)}+\frac{1}{\left(c-a\right)\left(b-c\right)\left(a+b+c\right)}\)\(+\frac{1}{\left(a-b\right)\left(c-a\right)\left(a+b+c\right)}\)
=\(\frac{c-a+a-b+b-c}{\left(b-c\right)\left(a-b\right)\left(a+b+c\right)}=0\)

Ta có :\(\left(a-b\right)\left(c^2+bc-a^2-ab\right)=\left(a-b\right)\left[\left(c^2-a^2\right)+\left(bc-ab\right)\right]\)
\(=\left(a-b\right)\left(c-a\right)\left(a+b+c\right)\)
Tương tự : \(\left(b-c\right)\left(a^2+ac-b^2-bc\right)=\left(b-c\right)\left(a-b\right)\left(a+b+c\right)\)
\(\left(c-a\right)\left(b^2+ab-c^2-ac\right)=\left(c-a\right)\left(b-c\right)\left(a+b+c\right)\)
\(MTC=\left(a-b\right)\left(b-c\right)\left(c-s\right)\left(a+b+c\right)\)
Kí hiệu biểu thức đã cho bởi \(Q\),ta có :
\(Q=\frac{c-a+a-b+b-c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)}=0\)

Bài 4:
\(\dfrac{x+1}{9}+\dfrac{x+2}{8}=\dfrac{x+3}{7}+\dfrac{x+4}{6}\)
\(\Leftrightarrow\left(\dfrac{x+1}{9}+1\right)+\left(\dfrac{x+2}{8}+1\right)=\left(\dfrac{x+3}{7}+1\right)+\left(\dfrac{x+4}{6}+1\right)\)
\(\Leftrightarrow\dfrac{x+10}{9}+\dfrac{x+10}{8}=\dfrac{x+10}{7}+\dfrac{x+10}{6}\)
\(\Leftrightarrow\dfrac{x+10}{9}+\dfrac{x+10}{8}-\dfrac{x+10}{7}-\dfrac{x+10}{6}=0\)
\(\Leftrightarrow\left(x+10\right)\left(\dfrac{1}{9}+\dfrac{1}{8}-\dfrac{1}{7}-\dfrac{1}{6}\right)=0\)
\(\Leftrightarrow x+10=0\) ( vì \(\dfrac{1}{9}+\dfrac{1}{8}-\dfrac{1}{7}-\dfrac{1}{6}\ne0\))
\(\Leftrightarrow x=-10\)
Vậy phương trình có tập nghiệm S =\(\left\{-10\right\}\)
Bài 1:
a: Thay x=3 vào pt, ta được:
\(12-2\left(1-3\right)^2=4\left(3-m\right)-\left(3-3\right)\left(2\cdot3+5\right)\)
=>4(3-m)=12-2*(-2)^2=12-2*4=12-8=4
=>3-m=1
=>m=2
b: Hai phương trình tương đương là hai phương trình có chung tập nghiệm
VD: x+2=0 và 2x+4=0

Ta có :
\(\frac{a}{ab+a+1}+\frac{b}{bc+b+1}+\frac{c}{ac+c+1}=\frac{abc}{ab^2c+abc+bc}+\frac{b}{bc+b+1}+\frac{bc}{abc+bc+b}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+b+1}\)
\(=\frac{bc+b+1}{bc+b+1}=1\) (đpcm)