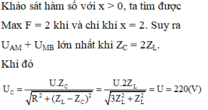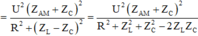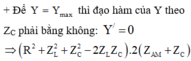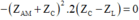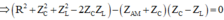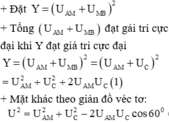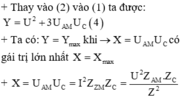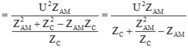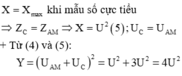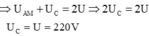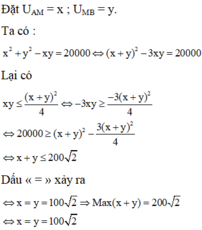Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Độ lệch pha giữa hai đầu đoạn mạch AM: tanφ AM = Z L R = tan 30 ° = 1 3 ⇒ Z L = R 3
Tổng trở của mạch AM: Z AM = R 2 + Z L 2 = 2 R 3 1
Đặt Y = U AM + U MB 2
Tổng U AM + U MB đạt giá trị cực đại khi Y đạt giá trị cực đại
Y = U AM + U MB 2 = I 2 Z AM + Z C 2 = U 2 Z AM + Z C 2 R 2 + Z L − Z C 2 = U 2 Z AM + Z C 2 R 2 + Z L 2 + Z C 2 − 2 Z L Z C
Để Y = Y max thì đạo hàm của Y theo Z C phải bằng không:
Y ' = 0 ⇒ R 2 + Z L 2 + Z C 2 − 2 Z L Z C . 2 Z AM + Z C − Z AM + Z C 2 . 2 Z C − Z L = 0
Ta lại có: Z AM + Z C ≠ 0 nên
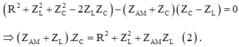
Thay (1) vào (2) ta được: Z C = 2 R 3 3
Tổng trở của toàn mạch: Z 2 = R 2 + Z L − Z C 2 ⇒ Z = 2 R 3
Ta thấy Z AM = Z MB = Z AB nên U MB = U C = U AB = 220 V

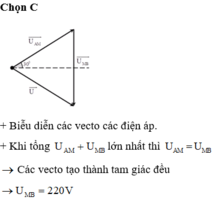
Đáp án C
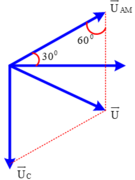
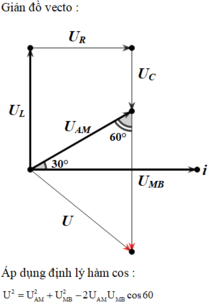
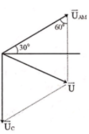
+ Biểu diễn vecto các điện áp: U A M → hợp với phương ngang của dòng điện một góc 30 ∘ , U M B → chứa tụ nên hướng thẳng đứng xuống dưới, U → = U A M → + U M B →
+ Áp dụng định lý sin trong tam giác, ta có:

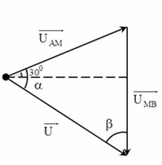

Đáp án B
+ Vẽ giản đồ vectơ như hình vẽ
+ Đặt ![]()
+ Tổng ![]() đạt giá trị cực đại khi Y đạt giá trị cực đại:
đạt giá trị cực đại khi Y đạt giá trị cực đại:
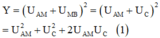
+ Mặt khác theo giản đồ ta có:
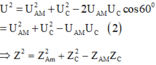
+ Thay (2) vào (1) ta được: ![]()
+ Ta có: ![]() có giá trị lớn nhất X=
X
max
có giá trị lớn nhất X=
X
max
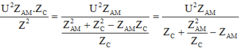
X=
X
max
khi mẫu số cực tiểu, suy ra: ![]()
+ Từ (4) và (5):
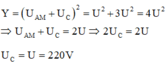

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u
Ta có giản đồ véc tơ như hình bên
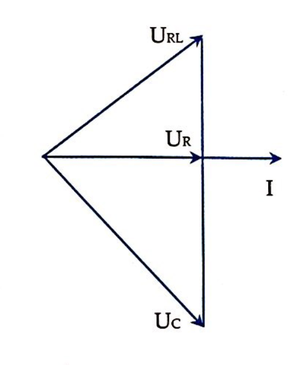
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 .6 U 0 R L 2 + 150 2 .6 U 0 2 = 1 1
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1 U 0 R L 2 + 1 U 0 2 = 1 U 0 R 2 = 1 150 2 .2 2
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 V