Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: I 0 = U 0 C L ⇒ U 0 = I 0 L C
Tại thời điểm năng lượng bằng năng lượng từ trường thì u = U 0 2 = I 0 2 L C = 0 , 06 2 . 80.10 − 3 5.10 − 6 = 5 , 366 V

\(\lambda=\frac{v}{f}\) có \(v=\cos st\) đẻ bước song tăng 2 lần thì \(f\) giảm 2 lần có \(f=\frac{1}{2.\pi.\sqrt{LC}}\) suy ra \(C\) tăng 4 lần
để \(C\) tăng phải mắc song song \(C_0=C_1+C_2\)
vậy đáp án là \(3C\)
\(\rightarrow C\)

Đáp án D
![]()
Sau khi dòng điện trong mạch ổn định, cắt nguồn thì mạch LC dao động với năng lượng :
![]()
![]()

Đáp án A
Khoảng thời gian ngắn nhất giữa hai lần năng lượng điện trường và năng lượng từ trường bằng nhau là: 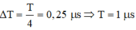
Năng lượng điện từ trong mạch:
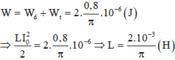
Điện dung của tụ điện:
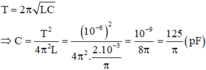

1. Cường độ dòng điện cùng pha với điện áp -> \(Z_L=Z_C\)
Nếu nối tắt tụ C thì mạch chỉ còn R nối tiếp với L.
\(\tan\varphi=\frac{Z_L}{R}=\tan\frac{\pi}{3}=\sqrt{3}\Rightarrow Z_L=\sqrt{3}.50=50\sqrt{3}\Omega\)
\(\Rightarrow Z_C=50\sqrt{3}\Omega\)
2. Cuộn dây phải có điện trở R
Ta có giản đồ véc tơ
Ud Uc Um 120 120 Ur 45 0
Từ giản đồ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
\(U_R=120\cos45^0=60\sqrt{2}V\)
Cường độ dòng điện: \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}V\)
Công suất: \(P=I^2R=I.U_R=0,6\sqrt{2}.60\sqrt{2}=72W\)

Đáp án B
Vì trong hai trường hợp, ở giản đồ vecto, ta có chúng vuông pha với nhau (vì sau T 4 ).
Vì vậy:
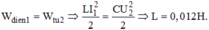
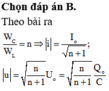


Đáp án A
Ta có: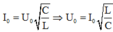
Tại thời điểm năng lượng bằng năng lượng từ trường thì