Cộng các phân số (rút gọn kết quả nếu có thể): 1 6 + - 5 6...

Cộng các phân số (rút gọn kết quả nếu có thể): 1 6...

SG

Sách Giáo Khoa

16 tháng 4 2017

Cộng các phân số (rút gọn kết quả nếu có thể)

a) $\dfrac{7}{-25}+\dfrac{-8}{25}$

b) $\dfrac{1}{6}+\dfrac{-5}{6}$

c) $\dfrac{6}{13}+\dfrac{-14}{39}$

d) $\dfrac{4}{5}+\dfrac{4}{-18}$

#Toán lớp 6

2

PT

Phan Thùy Linh

16 tháng 4 2017

Giải bài 42 trang 26 SGK Toán 6 Tập 2 | Giải toán lớp 6

Đúng(0)

PT

Phú Tuệ Minh

17 tháng 4 2017

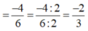
a. $\dfrac{-3}{5}$

b. $\dfrac{-2}{3}$ c. $\dfrac{4}{39}$ d. $\dfrac{26}{45}$

Đúng(0)

SG

Sách Giáo Khoa

15 tháng 5 2017

Cộng các phân số (rút gọn kết quả nếu có thể)

a) $\dfrac{1}{-5}+\dfrac{-5}{8}$

b) $\dfrac{4}{13}+\dfrac{-12}{39}$

c) $\dfrac{-1}{21}+\dfrac{-1}{28}$

#Toán lớp 6

1

BK

Bùi Khánh Thi

15 tháng 5 2017

Trả lời:

undefined

Đúng(0)

DN

Đoàn Như Quỳnh

3 tháng 3 2016 - olm

Câu 1: Cộng các phân số ( rút gọn kết quả nếu có thể):

a) $\frac{1}{6}$+$\frac{-5}{6}$ b) $\frac{6}{13}$+$\frac{-14}{39}$ c) $\frac{4}{5}$+$\frac{4}{-18}$

#Toán lớp 6

2

NT

Nguyen Thi Dieu Linh

3 tháng 3 2016

a)-2/3

b)4/39

c)26/45

Đúng(0)

HH

Hà Hà

3 tháng 3 2016

a) $\frac{1}{6}+\frac{-5}{6}$

$=\frac{1+\left(-5\right)}{6}$

$=\frac{-4}{6}=\frac{-2}{3}$

b) $\frac{6}{13}+\frac{-14}{39}$

$=\frac{18}{39}+\frac{-14}{39}$

$=\frac{4}{39}$

c) $\frac{4}{5}+\frac{4}{-18}$

$=\frac{4}{5}+\frac{-4}{18}$

$=\frac{72}{90}+\frac{-20}{90}$

$=\frac{52}{90}=\frac{26}{45}$

Đúng(0)

DN

Đoàn Như Quỳnh

3 tháng 3 2016 - olm

Cộng các phân số ( rút gọn kết quả nếu có thể ): $\frac{7}{-25}$+$\frac{-8}{25}$

#Toán lớp 6

6

LT

Lê thanh Dũng

3 tháng 3 2016

7/-25+-8/25=-7/25+-8/25=-15/25=-3/5

Đúng(0)

VT

VU THI XUAN MAI

3 tháng 3 2016

=-7/25+-8/25

=-15/25

=-3/5

k nha

Đúng(0)

B

binn2011

19 tháng 1 2017 - olm

Cộng các phân số ( rút gọn kết quả nếu có thể)

a, 7/-25 + -8/25

b, 1/6 + -5/6

c, 6/13 + -14/39

d, 4/5 + 4/-18

#Toán lớp 6

3

LM

Lê Mạnh Tiến Đạt

19 tháng 1 2017

a . 1/25

b . -2/3

c . 4/39

d . 26/45

Đúng(0)

CR

Cristiano Ronaldo

14 tháng 8 2017

giải.

a) $\frac{-3}{5}$ ; b) $\frac{-2}{3}$ ; c) $\frac{4}{39}$ ; d) $\frac{26}{45}$ .

Đúng(0)

CB

cún bông

27 tháng 2 2018 - olm

$\frac{-5}{12}+\frac{1}{-4}$

$\frac{5}{12}+\frac{-3}{28}$

$\frac{-7}{15}+\frac{3}{35}$

$\frac{-5}{7}+\frac{-3}{4}$

cộng ccas phân số ( rút gọn kết quả nếu có thể)

#Toán lớp 6

1

DL

Dương Lam Hàng

27 tháng 2 2018

$\frac{-5}{12}+\frac{-1}{4}=\frac{-5}{12}+\frac{-3}{12}=\frac{-5+-3}{12}=\frac{-8}{12}=\frac{-2}{3}$

$\frac{5}{12}+\frac{-3}{28}=\frac{35}{84}+\frac{-9}{84}=\frac{35+\left(-9\right)}{84}=\frac{26}{84}=\frac{13}{42}$

$\frac{-7}{15}+\frac{3}{35}=\frac{-49}{105}+\frac{9}{105}=\frac{-49+9}{105}=\frac{-40}{105}=\frac{-8}{21}$

$\frac{-5}{7}+\frac{-3}{4}=\frac{-20}{28}+\frac{-21}{28}=\frac{-20+\left(-21\right)}{28}=\frac{-41}{28}$

Đúng(0)

TN

Trần Ngọc Mai

29 tháng 2 2016 - olm

1. Cộng các phân số sau đây (rút gọn kết quả nếu có thể)

d) $\frac{7}{14}$+ $\frac{9}{-36}$ f) $\frac{-15}{24}$+ $\frac{18}{-42}$

#Toán lớp 6

2

TN

Trần Ngọc Mai

29 tháng 2 2016

giúp mình voi

Đúng(0)

NM

Nguyễn Mai Chi

16 tháng 2 2017

d)3/4

f)59/56

Đúng(0)

LR

lê ruby anna

22 tháng 3 2018 - olm

THỰC HIỆN PHÉP TÍNH (RÚT GỌN KẾT QUẢ NẾU CÓ THỂ)

1)$\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right).\left(\frac{3}{8}+\frac{34}{88}-\frac{345}{888}\right)$

2)$\frac{8}{3}.\frac{2}{5}.\frac{3}{8}.10.\frac{19}{92}$

#Toán lớp 6

2

PP

Pham Phan Anh Trieu

22 tháng 3 2018

(1/2-1/3-1/6).(3/8+34/88-345/888)

= (3/6-2/6-1/6).(3/8+34/88-345/888)

= 0.(3/8+434/88-345/888)=0

2. 8/3.2/5.3/8.10.19/92

= (8/3.3/8).(2/5.10).19/92

= 1.4.19/92

= 76/92

Đúng(0)

HP

Huỳnh Phước Mạnh

22 tháng 3 2018

1) $\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\left(\frac{3}{8}+\frac{34}{88}+\frac{345}{888}\right)=\left(\frac{3}{6}-\frac{2}{6}-\frac{1}{6}\right)\left(\frac{3}{8}+\frac{34}{88}+\frac{345}{888}\right)$

$=\left(\frac{1}{6}-\frac{1}{6}\right)\left(\frac{3}{8}+\frac{34}{88}+\frac{345}{888}\right)$

$=0\cdot\left(\frac{3}{8}+\frac{34}{88}+\frac{345}{888}\right)=0$(số nào nhân với 0 cũng bằng 0)

2) $\frac{8}{3}\cdot\frac{2}{5}\cdot\frac{3}{8}\cdot10\cdot\frac{19}{92}=\frac{8\cdot2\cdot3\cdot10\cdot19}{3\cdot5\cdot8\cdot92}$

$=\frac{2\cdot10\cdot19}{5\cdot92}=\frac{2\cdot2\cdot5\cdot19}{5\cdot2\cdot2\cdot23}=\frac{19}{23}$

Đúng(0)

LN

Lê Nam Khánh0103

18 tháng 6 2020 - olm

bài 1: phân số$\frac{n+9}{n-6}$(n thuộc N) có thể rút gọn cho số nào?

bài 2:tìm số tự nhiên n để phân số$\frac{18n+3}{\text{23n+7}}$có thể rút gọn được?

#Toán lớp 6

2

NL

Nguyễn Linh Chi

18 tháng 6 2020

1) Đặt: ( n + 9 ; n - 6 ) = d với d là số tự nhiên

=> $\hept{\begin{cases}n+9⋮d\\n-6⋮d\end{cases}}\Rightarrow\left(n+9\right)-\left(n-6\right)⋮d\Rightarrow15⋮d$

=> d $\in$Ư ( 15 ) = { 1; 3; 5; 15 }

=> d có thể rút gọn cho số 3; 5; 15

Đúng(0)

NL

Nguyễn Linh Chi

18 tháng 6 2020

2) Đặt: ( 18n + 3 ; 23n + 7 ) = d

=> $\hept{\begin{cases}18n+3⋮d\\23n+7⋮d\end{cases}}\Rightarrow23\left(18n+3\right)-18\left(23n+7\right)⋮d$

=> $57⋮d$

=> $d\inƯ\left(57\right)=\left\{1;3;19;57\right\}$

=> $\frac{18n+3}{\text{23n+7}}$ rút gọn được khi d = 3; d = 19 ; d = 57

Vì rút gọn được cho 57 thì sẽ rút gọn được cho 3 và cho 19

Nên mình chỉ cần xác định n với d = 3 và d =19

+) Với d = 3

$\hept{\begin{cases}18n+3⋮3\\23n+7⋮3\end{cases}}\Rightarrow9\left(18n+3\right)-7\left(23n+7\right)⋮3$

=> $n+11⋮3$

=> $n-1⋮3$

=>Tồn tại số tự nhiên k sao cho: $n=3k+1$khi đo phân số sẽ rút gọn được cho 3

+) Với d = 19

$\hept{\begin{cases}18n+3⋮19\\23n+7⋮19\end{cases}}\Rightarrow9\left(18n+3\right)-7\left(23n+7\right)⋮19$

=> $n+11⋮19\Rightarrow n-8⋮19$

=> Tồn tại số tự nhiên k sao cho n = 19k + 8 khi đó phân số sẽ rút gọn được cho 19

Vậy n = 3k + 1 hoặc n = 19k + 8 thì phân số sẽ rút gọn được.

Đúng(0)

PT

Pham Trong Bach

27 tháng 8 2019

Cộng các phân số (rồi rút gọn kết quả nếu có thể): 1 - 8 + - 5 8

#Toán lớp 6

1

CM

Cao Minh Tâm

27 tháng 8 2019

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP