Chứng minh rằng I = 1 + 3 + 3 2 + 3 3 + ....

Chứng minh rằng I = 1 + 3 + 3...

NC

❖︵Ňɠυүễη Çɦâυ Ƭυấη Ƙїệт♔

16 tháng 10 2018 - olm

Cho \(B=3+3^3+3^5+...3^{1991}\). Chứng minh rằng B chia hết cho 13 và chia hết cho 41

#Toán lớp 6

0

TT

Trần Tích Thường

13 tháng 10 2018 - olm

Cho B = \(3+3^3+3^5+....+3^{1991}\)Chứng minh rằng B chia hết cho 13 và 41

#Toán lớp 6

1

T

tth_new

13 tháng 10 2018

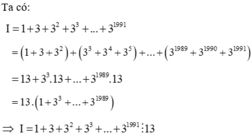
Ta có: \(B=3+3^3+3^5+...+3^{1991}\)

\(=\left(3+3^3+3^5\right)+\left(3^7+3^9+3^{11}\right)+...+\left(3^{1987}+3^{1989}+3^{1991}\right)\)

\(=3\left(1+3^2+3^4\right)+3^7\left(1+3^2+3^4\right)+...+3^{1987}\left(1+3^2+3^4\right)\)

\(=91\left(3+3^7+...+3^{1987}\right)⋮13^{\left(đpcm\right)}\)( vì 91 chia hết cho 33)

Phần còn lại chứng minh tương tự

Đúng(0)

NA

Nguyễn Anh Thư

22 tháng 2 2020 - olm

A= 2+2²+2³+2⁴+........+2⁵⁹+2⁶⁰

B= \(3+3^3+3^5+...+3^{1991}\)

Chứng minh rằng A chia hết cho 3, 7, 15

Chứng minh rằng B chia hết cho 13, 41

#Toán lớp 6

0

TT

Trịnh Thị Minh Ánh

1 tháng 10 2017

Bài 1 : Cho A = 13 + \(13^2+13^3+13^4+13^5+13^6.\) Chứng minh rằng A \(\)chia hết cho 2 . Bài 2 : Cho C = \(2+2^2+2^3+.....+2^{2011}+2^{2012}\). Chứng minh rằng C chia hết cho 3 . Bài 3 : Chứng minh rằng : A = \(2^1+2^2+2^3+.....+2^{59}+2^{60}\)chia hết cho 7 Bài 4 : Cho A = \(7+7^3+7^5+....+7^{1999}\) . Chứng minh rằng A chia hết cho 35 ...

Đọc tiếp

#Toán lớp 6

1

TM

Trần Minh Hoàng

1 tháng 10 2017

Vì 13 là lẻ \(\Rightarrow\) 13, 13², 13³, 13⁴, 13⁵, 13⁶ là lẻ.

Mà lẻ + lẻ + lẻ + lẻ + lẻ + lẻ = chẵn nên 13 + 13² + 13³ + 13⁴ + 13⁵ + 13⁶ là chẵn. \(\Rightarrow\) 13 + 13² + 13³ + 13⁴ + 13⁵ + 13⁶ \(⋮\) 2

\(\Rightarrow\) ĐPCM

Đúng(0)

QC

Quỳnh Châu

11 tháng 10 2016 - olm

Chứng minh rằng : I = 1 + 3 + 3²+ ... + 3¹⁹⁹¹ chia hết cho 13 và 41

#Toán lớp 6

1

I

♥ℒℴѵe♥

27 tháng 10 2017

l = 1 + 3 + 3² + ... + 3¹⁹⁹¹

l = (1 + 3 + 3²) + ... + (3¹⁹⁸⁹+ 3¹⁹⁹⁰ + 3¹⁹⁹¹)

l = 1.13 + ...+ 3¹⁹⁸⁹.13

l = 13.( 1 + .... + 3¹⁹⁸⁹)

=> I chia hết cho 13

Đúng(0)

NA

Nguyễn Anh Thư

22 tháng 2 2020 - olm

A= \(2+2^2+2^3+...+2^{60}\)

B= \(3+3^3+3^5+...+3^{1991}\)

Chứng minh A chia hết cho 3, 7, 15

Chứng minh B chia hết cho 13, 41

#Toán lớp 6

1

DT

Đoàn Thị Thảo Nguyên

22 tháng 2 2020

A = 2 + 2² + 2³ +......+ 2⁶⁰

-> A = ( 2 + 2² ) + ( 2³ + 2⁴ ) + ....+ ( 2⁵⁹ + 2⁶⁰ )

-> A = 2.( 1+2 ) + 2³.( 1+2) +......+ 2⁵⁹.( 1+2)

-> A = 2.3 + 2³.3 +......+ 2⁵⁹.3

-> A= 3.( 2 + 2³ +.....+ 2⁵⁹)

Vì 3 chia hết cho 3

-> 3.( 2 + 2³ +...+2⁵⁹⁾

Vậy A chia hết cho 3

A = 2 + 2² + 2³ +.......+ 2⁶⁰

-> A = ( 2 + 2² + 2³ ) +.......+ ( 2⁵⁸ + 2⁵⁹ + 2⁶⁰ )

-> A = 2.( 1 + 2 + 2² ) +......+ 2⁵⁸.( 1 + 2 + 2² )

-> A = 2.7 +.....+ 2⁵⁸.7

-> A = 7.( 2 + .....+ 2⁵⁸ )

Vì 7 chia hết cho 7

-> 7.( 2+....+ 2⁵⁸ )

Vậy A chia hết cho 7

A = 2 + 2² + 2³ +......+ 2⁶⁰

-> A = ( 2 + 2² + 2³ + 2⁴ ) +.....+ ( 2⁵⁷ + 2⁵⁸ + 2⁵⁹ + 2⁶⁰ )

-> A = 2.( 1 + 2 + 2² + 2³ ) +.....+ 2⁵⁷.( 1+ 2 + 2² + 2³ )

-> A = 2.15 + ......+ 2⁵⁷.15

-> A = 15.( 2 +.... + 2⁵⁷ )

Vì 15 chia hết cho 15

-> 15.( 2 +....+ 2⁵⁷ )

Vậy A chia hết cho 15

Đúng(0)

TT

Trịnh Thị Minh Ánh

1 tháng 10 2017

Bài 1 : Cho A = \(1+3+3^2+....+3^{11}\) . Chứng minh rằng : a) A chia hết cho 13 b) A chia hết cho 40 Bài 2 : Cho C = \(3+3^2+3^3+3^4+......+3^{100}\) . Chứng minh rằng : C chia hết cho 40 . Bài 3 : Cho biểu thức : M = \(1+3+3^2+3^3+......+3^{118}+3^{119^{ }}\) a) Thu gọn biểu thức M b) Biểu thức M có chia hết cho 5 , 13 không . Vì sao ? Bài 4 : Cho S = \(5+5^2+5^3+5^4+5^5+5^6+.......+5^{2012}\) . Chứng minh...

Đọc tiếp

#Toán lớp 6

2

TT

thám tử

1 tháng 10 2017

Bài 1 : \(A=1+3+3^2+...+3^{31}\)

a. \(A=\left(1+3+3^2\right)+...+3^9.\left(1.3.3^2\right)\)

\(\Rightarrow A=13+3^9.13\)

\(\Rightarrow A=13.\left(1+...+3^9\right)\)

\(\Rightarrow A⋮13\)

b. \(A=\left(1+3+3^2+3^3\right)+...+3^8.\left(1+3+3^2+3^3\right)\)

\(\Rightarrow A=40+...+3^8.40\)

\(\Rightarrow A=40.\left(1+...+3^8\right)\)

\(\Rightarrow A⋮40\)

Đúng(1)

TN

Trịnh Như Phương

1 tháng 10 2017

Bài 2:

Ta có: \(C=3+3^2+3^4+...+3^{100}\)

\(\Rightarrow C=(3+3^2+3^3+3^4)+...+(3^{97}+3^{98}+3^{99}+3^{100})\)

\(\Rightarrow3.(1+3+3^2+3^3)+...+3^{97}.(1+3+3^2+3^3)\)

\(\Rightarrow3.40+...+3^{97}.40\)

Vì tất cả các số hạng của biểu thức C đều chia hết cho 40

\(\Rightarrow C⋮40\)

Vậy \(C⋮40\)

Đúng(0)

NB

Nguyễn Boy Kênh Giang

7 tháng 11 2015 - olm

Chứng minh rằng : 1 + 3 + 3^2 + 3^3 + 3^4 + ....+ 3^1991 chia hết cho 13 và 41

#Toán lớp 6

1

HD

Hoàng Đức long

7 tháng 11 2015

A= 1 + 3 + 3^2 + 3^3 + 3^4 + ....+ 3^1991

A= (1 + 3 + 3^2) +( 3^3 + 3^4+3^5) + ....+(3^1989+3^1999+3^1991)

A= 13+3^3(1+3+3^2)+....+3^1989(1+3+3^2) chia hết cho 13

Còn 41 thì gộp 4 số rùi làm tương tự

Đúng(0)

NP

Nguyễn Phương Uyên

8 tháng 10 2017 - olm

a)cho A=2+2^2+2^3+...+2^60.chứng minh rằng A chia hết cho 3,7 và 15

b)cho B=3+3^3+3^4+...+3^1991.chứng minh rằng B chia hết cho 13 và 41

#Toán lớp 6

3

EF

Eternal friendship

15 tháng 12 2017

Ta có: A= 2 + 2²+ 2³+ ... + 2⁶⁰= (2 +2²) + (2³+ 2⁴) + ... + (2⁵⁹+ 2⁶⁰).

= 2 x (2 + 1) + 2³x (2 + 1) + ... + 2⁵⁹ x (2 + 1).

= 2 x 3 + 2³ x 3 + ... + 2⁵⁹x 3.

= 3 x ( 2 + 2³ + ... + 2⁵⁹).

Vì A = 3 x ( 2 + 2³ + ... + 2⁵⁹) nên A chia hết cho 3.

A= (2 +2²+ 2³) + (2⁴+ 2⁵ + 2⁶) + ... + (2⁵⁸ + 2⁵⁹+ 2⁶⁰).

= 2 x (1 + 2 + 2²) + 2⁴x (1 + 2 + 2²) + ... + 2⁵⁸ x (1 + 2 + 2²).

= 2 x 7 + 2⁴ x 7 + ... + 2⁵⁸x 7.

= 7 x ( 2 + 2⁴ + ... + 2⁵⁸).

Vì A = 7 x ( 2 + 2⁴ + ... + 2⁵⁸) nên A chia hết cho 7.

A= (2 +2²+ 2³+ 2⁴) + (2⁵+ 2⁶ + 2⁷+ 2⁸) + ... + (2⁵⁷+ 2⁵⁸ + 2⁵⁹+ 2⁶⁰).

= 2 x (1 + 2 + 2²+ 2³) + 2⁵x (1 + 2 + 2²+ 2³) + ... + 2⁵⁷ x (1 + 2 + 2²+ 2³).

= 2 x 15 + 2⁵ x 15 + ... + 2⁵⁷x 15.

= 15 x ( 2 + 2⁴ + ... + 2⁵⁸).

Vì A = 15 x ( 2 + 2⁴ + ... + 2⁵⁸) nên A chia hết cho 15.

Ta có: B= 3 + 3³+ 3⁵+ ... + 3¹⁹⁹¹= (3 + 3³+ 3⁵) + (3⁷+ 3⁹+ 3¹¹ ) + ... + (3¹⁹⁸⁷+ 3¹⁹⁸⁹+ 3¹⁹⁹¹).

= 3 x (1 + 3²+ 3⁴) + 3⁷x (1 + 3²+ 3⁴) + ... + 3¹⁹⁸⁷ x (1 + 3²+ 3⁴).

= 3 x 91 + 3⁷ x 91 + ... + 3¹⁹⁸⁷x 91= 3 x 7 x 13 + 3⁷ x 7 x 13 + ... + 3¹⁹⁸⁷ x 7 x 13.

= 13 x ( 3x 7 + 3⁷ x 7 + ... + 3¹⁹⁸⁷x 7).

Vì B = 13 x ( 3x 7 + 3⁷ x 7 + ... + 3¹⁹⁸⁷x 7) nên B chia hết cho 13.

B= (3 + 3³+ 3⁵+ 3⁷) + ... + (3¹⁹⁸⁵+ 3¹⁹⁸⁷+ 3¹⁹⁸⁹+ 3¹⁹⁹¹).

= 3 x (1 + 3²+ 3⁴ + 3⁶) + ... + 3¹⁹⁸⁵ x (1 + 3²+ 3⁴+ 3⁶).

= 3 x 820 + ... + 3¹⁹⁸⁵x 820= 3 x 20 x 41 + ... + 3¹⁹⁸⁵ x 20 x 41.

= 41 x ( 3 x 20 + .. + 3¹⁹⁸⁵ x 20)

Vì B =41 x ( 3 x 20 + .. + 3¹⁹⁸⁵ x 20) nên B chia hết cho 41.

Đúng(0)

A

Ad

14 tháng 10 2018

a) Ta có: \(A=3+3^3+3^5+...+3^{1991}\)

\(=\left(3+3^3+3^5\right)+\left(3^7+3^9+3^{11}\right)+...+\left(3^{1987}+3^{1989}+3^{1991}\right)\)

\(=3\times\left(1+3^2+3^4\right)+3^7\times\left(1+3^2+3^4\right)+...+3^{1987}\times\left(1+3^2+3^4\right)\)

\(=3\times91+3^7\times91+...+3^{1987}\times91\)

\(=3\times7\times13+3^7\times7\times13+...+3^{1987}\times7\times13\)

\(=13\times\left(3\times7+3^7\times7+...+3^{1987}\times7\right)\)

Vì \(A=13\times\left(3\times7+3^7\times7+...+3^{1987}\times7\right)\)nên A chia hết cho 13.

b) Ta có: \(A=3+3^3+3^5+...+3^{1991}\)

\(=\left(3+3^3+3^5+3^7\right)+...+\left(3^{1985}+3^{1987}+3^{1989}+3^{1991}\right)\)

\(=3\times\left(1+3^2+3^4+3^6\right)+...+3^{1985}\times\left(1+3^2+3^4+3^6\right)\)

\(=3\times820+...+3^{1985}\times820\)

\(=3\times20\times41+...+3^{1985}\times20\times41\)

\(=41\times\left(3\times20+...+3^{1985}\times20\right)\)

Vì \(A=41\times\left(3\times20+...+3^{1985}\times20\right)\)nên A chia hết cho 41.

Đúng(1)

NT

Nguyễn Thị Kim Anh

3 tháng 10 2015 - olm

Cho A = 2+2^2+2^3+...+2^60 . chứng minh rằng A chi hết cho 3,7 và 15.
Cho B = 3+ 3^3+3^5+.....+3^1991. Chứng minh rằng B chia hết cho 13 và 41

#Toán lớp 6

2

KI

kurosaki ichigo

3 tháng 10 2015

A={2+2^2}+{2^3+2^4}+.......+{2^59+2^60}

={2.1+2.2}+{2^3.1+2^3.2}+....+{2^59.1+2^59.2}

=2{1+2}+2^3{1+2}+...+2^59{1+2}

=2.3+2^3.3+.....+2^59.3

=3.(2+2^3+...+2^59)

vi co thua so 3 => tich do chia het cho 3

Đúng(0)

NT

Nguyễn Trọng Phúc

12 tháng 10 2022

A={2+2^2}+{2^3+2^4}+.......+{2^59+2^60}

={2.1+2.2}+{2^3.1+2^3.2}+....+{2^59.1+2^59.2}

=2{1+2}+2^3{1+2}+...+2^59{1+2}

=2.3+2^3.3+.....+2^59.3

=3.(2+2^3+...+2^59)

vi co thua so 3 => tich do chia het cho 3

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP