
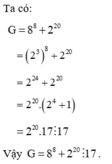
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

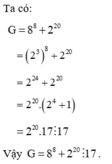

\(=\left(2^3\right)^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}.\left(2^4+1\right)\)\(=2^{20}.17⋮17\)
Vậy ...
88 + 220
= (23)8 + 220
= 224 + 220
= 220.24 + 220.1
= 220(24 + 1)
= 220.17 ⋮ 17 (đpcm)

Ta có:
A=88+220
=(23)8+220
=224+220
=220.24+220
=220.(24+1)
=220.(16+1)
=220.17 chia hết cho 17
Vậy A=88+220 chia hết cho 17
Tick nha
\(A=8^8+2^{20}=\left(2^3\right)^8+2^{20}=2^{24}+2^{20}=2^{20}.2^4+2^{20}\)
A= \(2^{20}.\left(2^4+1\right)=2^{20}.17\) chia het cho 17(đpcm)
tick nhé ban

Ta có:
88 + 220
= (23)8 + 220
= 23 . 8 + 220
= 220 . 24 + 220
= 220 . (16 + 1)
= 220 . 17 \(⋮\) 17(đpcm)

Bài 78 :
Số có tận cùng là 1 khi nâng lên lũy thừa vẫn có tận cùng là 1
Ta có : A có 10 số hạng
Vậy A = (...1) + (...1) + .... + (..1) = (...0)
A có chữ số tận cùng là 0 nên A chia hết cho 5
78/ \(A=11^9+11^8+11^7+...+11+1\)
\(\Rightarrow2A=11^{10}+11^9+11^8+11^7+...+11\)
\(\Rightarrow2A\text{-}A=\left(11^{10}+11^9+11^8+11^7+...+11\right)\text{-}\left(+11^9+11^8+11^7+...+11+1\right)\)
\(A=11^{10}\text{-}1\)
\(A=\left(...1\right)\text{-}1\Rightarrow A=\left(...0\right)\)tận cùng là 0 chia hết cho 5.



88 + 410
= ( 23)8 + 410
= 224 + 410
= 220 x 24 + 410
= 220 x ( 410 + 1 )
= 220 x 17 nếu nhân ra kết quả mà chia hết cho 17 thì số đó chia hết cho 17

\(B=8^8+2^{20}\)
\(\Rightarrow B=2^{24}+2^{20}\)
\(\Rightarrow B=2^{20}.\left(2^4+1\right)\)
\(\Rightarrow B=2^{20}.17⋮17\)

a) \(A=1+2+3^2+....+3^{11}\)
\(=\left(1+3\right)+\left(3^2+3^3\right)+...+\left(3^{10}+3^{11}\right)\)
\(=\left(1+3\right)+3^2\left(1+3\right)+....+3^{10}\left(1+3\right)\)
\(=\left(1+3\right)\left(1+3^2+...+3^{10}\right)\)
\(=4\left(1+3^2+...+3^{10}\right)\)\(⋮\)\(4\)
b) \(B=16^5+2^{15}=\left(2^4\right)^5+2^{15}=2^{20}+2^{15}=2^{15}.\left(2^5+1\right)=2^{15}.33\)\(⋮\)\(33\)
c) \(C=10^{28}+8=1000...008\)(27 chữ số 0)
Nhận thấy: tổng các chữ số của C chia hết cho 9 => C chia hết cho 9
3 chữ số tận cùng của C chia hết cho 8 => C chia hết cho 8
mà (8;9) = 1 => C chia hết cho 72
d) \(D=8^8+2^{20}=2^{24}+2^{20}=2^{20}\left(2^4+1\right)=2^{20}.17\)\(⋮\)\(17\)