Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha!
a) Ta có: \(\widehat{xOy}+\widehat{OMt}=120^0+60^0=180^0\)
Mà 2 góc này nằm ở vị trí trong cùng phía
=> \(Oy\) // \(Mt.\)
b) Bạn xem lại đề đi, hình như bị sai rồi.
Chúc bạn học tốt!

t x u m y m' M O 120 60
a) Vì \(\widehat{mMO}\) và \(\widehat{MOy}\) là 2 góc trong cùng phía
mà \(\widehat{mMO}+\widehat{MOy}=60^0+120^0=180^0\)
\(\Rightarrow Oy\) // Mm (đpcm)
Vậy Oy // Mm
b) Vì Ou là tia phân giác \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOu}=\widehat{uOy}=\dfrac{1}{2}.\widehat{xOy}=\dfrac{1}{2}.120^0=60^0\)
Ta có: \(\widehat{m'MO}+\widehat{OMm}=180^0\) ( 2 góc kề bù)
\(\Rightarrow\widehat{OMm'}=180^0-\widehat{OMm}\)
\(\Rightarrow\widehat{OMm'}=180^0-60^0=120^0\)
Vì Mt là tia phân giác \(\widehat{OMm'}\)
\(\Rightarrow\widehat{m'Mt}=\widehat{tMO}=\dfrac{1}{2}.\widehat{m'MO}=\dfrac{1}{2}.120^0=60^0\)
Vì \(\widehat{tMO}\) và \(\widehat{xOu}\) là 2 góc so le trong
mà \(\widehat{tMO}=\widehat{xOu}\left(=60^0\right)\)
\(\Rightarrow Mt\) // Ou (đpcm)
Vậy Mt // Ou

x O y A z z' N M
Giải:
a) Vì \(\widehat{xOy}+\widehat{OAz}=180^o\) và 2 góc này nằm cùng phía nên Az // Oy hay zz' // Oy ( đpcm )
b) Vì OM là tia phân giác của \(\widehat{xOy}\) nên
\(\widehat{xOM}=\frac{1}{2}.\widehat{xOy}=75^o\)
Ta có: \(\widehat{xAz}+\widehat{zAO}=180^o\)
\(\Rightarrow\widehat{xAz}+30^o=180^o\)
\(\Rightarrow\widehat{xAz}=150^o\)
Vì AN là tia phân giác của \(\widehat{xAz}\) nên
\(\widehat{xAN}=\frac{1}{2}.\widehat{xAz}=75^o\)
Ta thấy \(\widehat{xOM}=\widehat{xAN}\left(=75^o\right)\) và 2 góc này ở vị trí đồng vị nên AN // OM (đpcm)

120 y x m y' m d c O
a) Ta có: \(\widehat{xOy}=120^o\)
có Om là tia phân giác
=> \(\widehat{mOy}=\widehat{mOx}=120^o:2=60^o\)
Oy' là tia đối tia Oy
=> \(\widehat{yOy'}=180^o\)
=> \(\widehat{xOy'}=\widehat{yOy'}-\widehat{yOx}=180^o-120^o=60^o\)
=> \(\widehat{xOy'}=\widehat{xOm}=60^o\)
Mặt khác Ox nằm giữa hai tia Om, Oy'
=> Õx là phân giác góc y'Om
b) Ta có: Od nằm phóa ngoài góc xOy
Oy' nằm phía ngoài góc xOy
Mà \(\widehat{xOy'}=60^o< 90^o=\widehat{xOd}\)
=> Oy' nằm giữa hai tia Ox, Od
c) \(\widehat{mOc}=\widehat{mOy}+\widehat{yOc}=60^o+90^o=150^o\)
d) Ta có: On là phân giác góc dOc
mà \(\widehat{dOc}=360^o-\widehat{xOy}-\widehat{xOd}-\widehat{yOc}=60^o\)
=>\(\widehat{dOn}=\widehat{nOc}=60^o:2=30^o\)
=> \(\widehat{mOn}=\widehat{mOc}+\widehat{cOn}=150^O+30^O=180^O\)

cái đề dài thế này, chả biết khó hay ko nhưng mà ngại làm quá :[
hình như câu b cho đề sai, pải là: ∆EAB=∆ECD mới đúng

Xét tam giác AOC và tam giác BOC có:
AO = BO (gt)
AOC = BOC (OC là tia phân giác của AOB)
OC là cạnh chung
=> Tam giác AOC = Tam giác BOC (c.g.c)
OA = OB (gt)
=> Tam giác OAB cân tại O
mà OI là tia phân giác của AOB
=> OI là đường trung trực của tam giác OAB
=> I là trung điểm của AB
OI _I_ AB
Ta có hình vẽ:
x O y z A B C I
Vì Oz là phân giác của xOy nên \(xOz=zOy=\frac{xOy}{2}\)
Xét Δ AOC và Δ BOC có:
OA = OB (gt)
góc AOC = góc BOC (chứng minh trên)
OC là cạnh chung
Do đó, Δ AOC = Δ BOC (c.g.c) (đpcm)
Vì Δ AOC = Δ BOC nên AC = BC (2 cạnh tương ứng)
góc ACO = góc BCO (2 góc tương ứng)
Xét Δ AIC và Δ BIC có:
AC = BC (chứng minh trên)
góc ACI = BCI (chứng minh trên)
CI là cạnh chung
Do đó, Δ AIC = Δ BIC (c.g.c)
=> AI = IB (2 cạnh tương ứng)
=> I là trung điểm của đoạn AB (đpcm)
Vì Δ AIC = Δ BIC nên góc AIC = BIC (2 góc tương ứng)
Lại có: AIC + BIC = 180o (kề bù)
Do đó, góc AIC = góc BIC = 90o
=> \(AB\perp OC\left(đpcm\right)\)
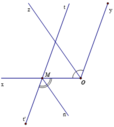

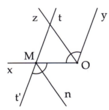
a) Ta có: O M t ^ + x O y ^ = 70 0 + 110 0 = 180 0 .
Mà hai góc này ở vị trí trong cùng phía nên Mt // Oy
b) Ta có Oz là tia phân giác của x O y ^ nên x O z ^ = x O y ^ 2 = 110 0 2 = 55 0 (1)
Vì Mt’ là tia đối của tia Mt nên: t M O ^ + O M t ' ^ = 180 0 ⇒ 70 0 + O M t ' ^ = 180 0 ⇒ O M t ' ^ = 110 0
Mà Mn là tia phân giác của O M t ' ^ nên
O M n ^ = O M t ' ^ 2 = 110 0 2 = 55 0 (2)
Từ (1) và (2) suy ra x O z ^ = O M n ^ .
Mà hai góc này ở vị trí so le trong nên Mn //Oz