Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TenAnh1
TenAnh1
A = (-0.14, -7.4)
A = (-0.14, -7.4)
A = (-0.14, -7.4)
B = (14.46, -7.36)
B = (14.46, -7.36)
B = (14.46, -7.36)
C = (-3.74, -5.6)
C = (-3.74, -5.6)
C = (-3.74, -5.6)
D = (11.62, -5.6)
D = (11.62, -5.6)
D = (11.62, -5.6)
E = (-3.34, -5.86)
E = (-3.34, -5.86)
E = (-3.34, -5.86)
F = (12.02, -5.86)
F = (12.02, -5.86)
F = (12.02, -5.86)
G = (-3.7, -5.88)
G = (-3.7, -5.88)
G = (-3.7, -5.88)
H = (11.66, -5.88)
H = (11.66, -5.88)
H = (11.66, -5.88)
a) Các véctơ cùng phương với là:
,
,
,
,
,
,
.
b) Các véctơ cùng hướng với là:
,
,
.
c) Các véctơ ngược hướng với là:
,
,
,
.

1/ \(\overrightarrow{AB}^2-\overrightarrow{AD}^2=\overrightarrow{BC}^2-\overrightarrow{CD}^2\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=\left(\overrightarrow{BC}+\overrightarrow{CD}\right)\left(\overrightarrow{BC}-\overrightarrow{CD}\right)\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right).\overrightarrow{DB}=\overrightarrow{BD}\left(\overrightarrow{BC}-\overrightarrow{CD}\right)=\overrightarrow{DB}\left(\overrightarrow{CB}+\overrightarrow{CD}\right)\)
Gọi M là trung điểm BD
\(\Rightarrow2\overrightarrow{AM}.\overrightarrow{DB}=2\overrightarrow{CM}.\overrightarrow{DB}\)
\(\Leftrightarrow\overrightarrow{DB}.\left(\overrightarrow{AM}-\overrightarrow{CM}\right)=0\)
\(\Leftrightarrow\overrightarrow{BD}.\overrightarrow{AC}=0\)
2/ \(A=\left|\overrightarrow{a}-\overrightarrow{b}\right|\Rightarrow A^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\)
\(=a^2+b^2-2ab.cos\left(\overrightarrow{a};\overrightarrow{b}\right)=4^2+5^2-2.4.5.cos120^0=61\)
\(\Rightarrow A=\sqrt{61}\)
b/ \(B=\left|2\overrightarrow{a}+\overrightarrow{b}\right|\Rightarrow B^2=4a^2+b^2+4\overrightarrow{a}.\overrightarrow{b}\)
\(=4a^2+b^2+4ab.cos120^0=49\)
\(\Rightarrow B=7\)
3/ \(\left|\overrightarrow{x}\right|=\left|\overrightarrow{a}-2\overrightarrow{b}\right|\Rightarrow\left|\overrightarrow{x}\right|^2=a^2+4b^2-4\overrightarrow{a}.\overrightarrow{b}=12\)
\(\Rightarrow\left|\overrightarrow{x}\right|=2\sqrt{3}\)
\(\left|\overrightarrow{y}\right|^2=a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=5\Rightarrow\left|\overrightarrow{y}\right|=\sqrt{5}\)
\(\overrightarrow{x}.\overrightarrow{y}=\left(\overrightarrow{a}-2\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=a^2+2b^2-3\overrightarrow{a}.\overrightarrow{b}=4\)
\(\Rightarrow cos\alpha=\frac{\overrightarrow{x}.\overrightarrow{y}}{\left|\overrightarrow{x}\right|.\left|\overrightarrow{y}\right|}=\frac{4}{2\sqrt{15}}=\frac{2\sqrt{15}}{15}\)

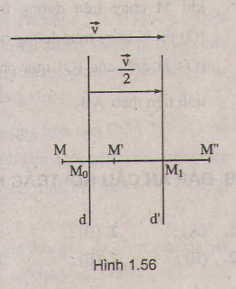
Lấy M tùy ý. Gọi (M) = M',
(M') = M''. Ta có
\(\overrightarrow{MM'}=\overrightarrow{MM'}+\overrightarrow{M'M''}=2\overrightarrow{M_oM'}+2\overrightarrow{M'M_1}=2\overrightarrow{M_oM_1}\)\(=2\dfrac{\overrightarrow{v}}{2}=\overrightarrow{v}\).
Vậy M'' = (M) =
(
(M)), với mọi M
Do đó phép tịnh tiến theo vectơ v là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d'.
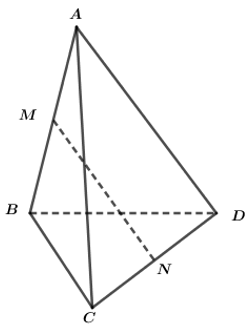




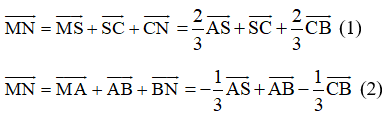
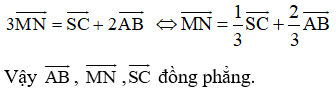
\(\dfrac{MA}{MB}=k\Rightarrow MA=kMB=k\left(AB-AM\right)\Rightarrow MA=\dfrac{k}{k+1}AB\)
\(\Rightarrow\overrightarrow{MA}=\dfrac{k}{k+1}\overrightarrow{BA}\)
Tương tự: \(\overrightarrow{CN}=\dfrac{k}{k+1}\overrightarrow{CD}\)
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{CN}=\dfrac{k}{k+1}\overrightarrow{BA}+\overrightarrow{AC}+\dfrac{k}{k+1}\overrightarrow{CD}\)
\(=\dfrac{k}{k+1}\left(\overrightarrow{BD}+\overrightarrow{DA}\right)+\overrightarrow{AC}+\dfrac{k}{k+1}\overrightarrow{CD}\)
\(=\dfrac{k}{k+1}\overrightarrow{BD}+\dfrac{k}{k+1}\left(\overrightarrow{CD}+\overrightarrow{DA}\right)+\overrightarrow{AC}\)
\(=\dfrac{k}{k+1}\overrightarrow{BD}-\dfrac{k}{k+1}\overrightarrow{AC}+\overrightarrow{AC}\)
\(=\dfrac{k}{k+1}\overrightarrow{BD}+\dfrac{1}{k+1}\overrightarrow{AC}\)