Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

I là tâm đường tròn nội tiếp tam giác và E là tiếp điểm
nên IE⊥AC, mà A^=90o suy ra IE//AB
⇒ANEI=AMEM
⇒AN=AM.EIEM=AC.EI2(AM−AE) (1)
Tứ giác AEIF là hình vuông nên AE=EI;
D, E, F là các tiếp điểm
⇒AE+CD+BD=12(BC+CA+AB)⇒AE=AC+AB−BC2,
thay vào (1) ta được ...

Hướng dẫn làm bài:
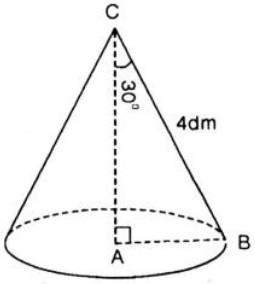
Trong tam giác vuông ABC, ta có:
AB=BC.sinC=BC.sin300=4.1/2=2(dm)
AC=BC.cosC=BC.cos300=4.√3/2=2√3(dm)
Ta có: Sxq = πRl = π. 2. 4 = 8 π (dm2)
V=1/3 π R2 h=1/3 π.22.2√3=8√3.π/3(dm3)

Giải chi tiết:
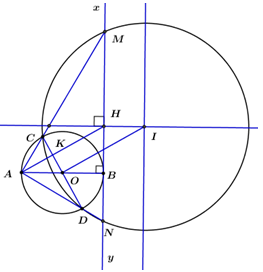
1) Chứng minh tứ giác MCDN nội tiếp.
Xét (O;R)(O;R) ta có: AB,CDAB,CD là hai đường kính của hình tròn
⇒ADBC⇒ADBC là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi đường).
⇒{AC=BDAD=BC⇒{AC=BDAD=BC (các cạnh đối).
Ta có: ∠ADB=900∠ADB=900 (góc nội tiếp chắn nữa đường tròn)
⇒∠BDN=900(1)⇒∠BDN=900(1)
Ta có: ∠CMN∠CMN là góc có đỉnh nằm ngoài đường tròn chắn các cung
BCBC và AB.AB.
⇒∠CMN=12(sdcungAB−sdcungCB)=12sdcungBD=12sdcungAC.(doAC=BD)⇒∠CMN=12(sdcungAB−sdcungCB)=12sdcungBD=12sdcungAC.(doAC=BD)
Lại có: ∠ADC∠ADC là góc nội tiếp chắn cung AC⇒∠ADC=12sdcungACAC⇒∠ADC=12sdcungAC
⇒∠ADC=∠CMN(=12sdcungAC).⇒∠ADC=∠CMN(=12sdcungAC).
⇒CDNM⇒CDNM là tứ giác nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện). (đpcm)
2) Chứng minh AC.AM=AN.AN.AC.AM=AN.AN.
Xét ΔACDΔACD và ΔANMΔANM ta có:
∠CADchung∠AMB=∠ADC(cmt)⇒ΔACD∼ΔANM(g−g)⇒ACAN=ADAM⇒AC.AM=AN.AD(dpcm).∠CADchung∠AMB=∠ADC(cmt)⇒ΔACD∼ΔANM(g−g)⇒ACAN=ADAM⇒AC.AM=AN.AD(dpcm).
3) Gọi I là tâm đường tròn nội tiếp tứ giác MCDN và H là trung điểm MN. Chứng minh tứ giác AOIH là hình bình hành. Khi đường kính CD quay quanh điểm O thì I di động trên đường nào?
Ta có I là tâm đường tròn nội tiếp tứ giác MCDN, H là trung điểm của MN
⇒IH⊥MN⇒IH⊥MN (mối quan hệ giữa đường kính và dây cung).
Mà AO⊥MNAO⊥MN (do AB là đường kính của đường tròn (O), MN là tiếp tuyến tại B của đường tròn)
⇒HI//AO(⊥MN)(1)⇒HI//AO(⊥MN)(1)
Mặt khác ta có ∠CAD=900∠CAD=900 (góc nội tiếp chắn nửa đường tròn)
⇒∠ACD+∠CDA=900⇒∠ACD+∠CDA=900 (tổng hai góc nhọn trong tam giác vuông)
Xét ΔMANΔMAN có ∠MAN=900∠MAN=900, H là trung điểm của MN
⇒AH=12MN=MH⇒AH=12MN=MH (đường trung tuyến ứng với cạnh huyền của tam giác vuông)
⇒ΔAHM⇒ΔAHM cân tại H (dhnb)
⇒∠MAH=∠HMA⇒∠MAH=∠HMA (hai góc kề đáy của tam giác cân).
Lại có : ∠ACD=∠CAB∠ACD=∠CAB (hai góc nội tiếp chắn hai cung AD, CB bằng nhau).
Mà : ∠AMH+∠CAB=900∠AMH+∠CAB=900 (tam giác ABM vuông tại B)
⇒∠MAH+∠ACD=900⇒ΔCAK⇒∠MAH+∠ACD=900⇒ΔCAK vuông tại K⇒CD⊥AH={K}.K⇒CD⊥AH={K}.
Lại có : OI⊥CDOI⊥CD (mối quan hệ giữa đường kính và dây cung)
⇒AH//OI(⊥CD).(2)⇒AH//OI(⊥CD).(2)
Từ (1) và (2) ta có : {AH//OIAO//HI⇒AOIH{AH//OIAO//HI⇒AOIH là hình bình hành (dhnb). (đpcm)
Ta có : HH là trung điểm của MN,M,NMN,M,N thuộc đườn thẳng xyxy cố định ⇒H⇒H là điểm di động trên đường xy.xy.
Vì AOIHAOIH là hình bình hành (cmt) ⇒AO=IH⇒AO=IH (hai cạnh đối)
Mà AO=RAO=R không đổi ⇒IH=R⇒IH=R không đổi.
⇒I⇒I là điểm di động trên đườgn thẳng song song với đường thẳng xy.xy.
4) Khi góc AHB bằng 600; Tính diện tích xung quanh của hình trụ tạo thành khi hình bình hành AHOI quay quanh cạnh AH theo R.
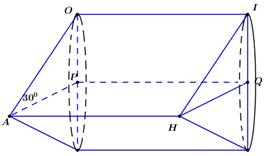
Ta có : ∠AHB=600⇒∠OAH=300∠AHB=600⇒∠OAH=300
Khi quay hình bình hành AHIO một vòng quanh cạnh AH thì cạnh AO và cạnh HI tạo nên hai hình nón bằng nhau có đường sinh AO=IH=R.AO=IH=R.
Cạnh OI tạo nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón cũng như bán kính của hình tròn (O)(O) là R.R.
Gọi P, Q là tâm các đường tròn đáy của hình trụ.
Xét ΔAOPΔAOP ta có : ∠OPA=900,∠OAP=300.∠OPA=900,∠OAP=300.
⇒sin300=OPOA=OPR⇒OP=Rsin300=R2.⇒sin300=OPOA=OPR⇒OP=Rsin300=R2.
Xét ΔABHΔABH ta có : AH=ABtan600=2R√3=2R√33.AH=ABtan600=2R3=2R33.
Diện tích xung quanh hình trụ cần tính là : Sxq=2πrh=2π.OP.AH=2π.R2.2R√33=2πR2√33.

4. Dễ thấy \(\Delta AML\approx\Delta LKC\left(g-g\right)\)
\(\Rightarrow\frac{AL}{LC}=\sqrt{\frac{S_{\Delta AML}}{S_{\Delta LKC}}}=\sqrt{\frac{42.7283}{51.4231}}\approx0.9115461896\)
\(\Rightarrow\frac{AL}{AC}=\frac{0.9115461896}{0.9115461896+1}=0.476863282\)
Lại có \(\Delta AML\approx\Delta ABC\left(g-g\right)\)
\(\Rightarrow\frac{S_{AML}}{S_{ABC}}=\left(\frac{AL}{AC}\right)^2=0.476863282^2=0.2273985897\)
\(\Rightarrow S_{\Delta ABC}=\frac{S_{\Delta AML}}{0.2273985897}=\frac{42.7283}{0.2273985897}\approx187.9\left(cm^2\right)\)
1. Ta có \(\frac{BH}{CH}=\frac{\sqrt{7}}{\sqrt{5}}\Rightarrow BH=\frac{\sqrt{7}}{\sqrt{5}}CH\)
Mặt khác \(BC=\sqrt{11}\Rightarrow BH+CH=11\)
\(\Rightarrow\frac{\sqrt{7}}{\sqrt{5}}CH+CH=11\)
\(\Leftrightarrow CH=\frac{-55+11\sqrt{35}}{2}\) và \(BH=\frac{77-11\sqrt{35}}{2}\)
Có BH, CH và BC tính đc AB, AC \(\left(AB=\sqrt{BH.BC};AC=\sqrt{CH.BC}\right)\)
Từ đó tính đc chu vi tam giác ABC.
2. Để cj gửi hình qua gmail cho
3. Chỉ còn cách làm từng bước thôi e
\(B=31+\frac{27}{\frac{30127}{2008}}=31+\frac{54216}{30127}=32+\frac{24089}{30127}\)
Để viết liên phân số, ta bấm phím tìm thương và số dư:
(Mỗi số b1, b2, b3, ..., bn-1 chính là thương; số chia của phép chia trước là số bị chia của phép chia sau, còn số dư của phép chia trước là số chia của phép chia sau, nhớ nhá)
- B1: Tìm thương và số dư của 30127 cho 24089, thương là 1, dư 6038, viết \(B=32+\frac{1}{1+...}\)
- B2: Tìm thương và số dư của 24089 cho 6038, thương là 3, dư 5975, viết \(B=32+\frac{1}{1+\frac{1}{3+...}}\)
- B3: Tìm thương và số dư của 6038 cho 5975, thương là 1, dư 63, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+...}}}\)
- B4: Tìm thương và số dư của 5975 cho 63, thương là 94, dư 53, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+...}}}}\)
...
Cứ làm như vậy, đến khi số dư là 1 thì dừng lại, phân số cuối cùng \(\frac{1}{b_n}\) thì bn chính là số chia cuối cùng, bn = 3
Kết quả: \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+\frac{1}{1+\frac{1}{5+\frac{1}{3+\frac{1}{3}}}}}}}}\)

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

