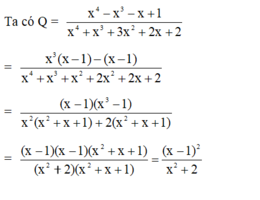Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,-x^2+6x-16\)
\(=-x^2+3x+3x-9-5\)
\(=-x\left(x-3\right)+3\left(x-3\right)-5\)
\(=\left(3-x\right)\left(x-3\right)-5\)
\(=-\left(x-3\right)^2-5\le-5\)=>Luôn âm
\(c,-1+x-x^2\)
\(=-x^2+x-1\)
\(=-\left(x^2-x+\frac{1}{2}+\frac{1}{2}\right)\)
\(=-\left(x-\frac{1}{2}\right)^2-\frac{1}{2}\le\frac{-1}{2}\)=>Luôn âm

a,\(-\left(x^2-3x+4\right)\)
\(-\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]\)
\(\Leftrightarrow-\left(x-\frac{3}{2}\right)^2-\frac{7}{4}\le-\frac{7}{4}\)(luôn âm)
b\(-2\left(x^2-5x+\frac{15}{2}\right)\)
\(-2\left[\left(x-\frac{5}{2}\right)^2+\frac{5}{4}\right]\)
\(-2\left(x-\frac{5}{4}\right)^2-\frac{5}{2}\le-\frac{5}{2}\)(luôn âm)
c,\(-\left[\left(4x^2-4x+1\right)+\left(2y^2-6y+5\right)\right]\)
\(=-\left[\left(2x-1\right)^2+2\left(y^2-3y+\frac{5}{2}\right)\right]\)
\(=-\left[\left(2x-1\right)^2+2\left(y-\frac{3}{2}\right)^2+\frac{1}{4}\right]\)
\(=-\left[\left(2x-1\right)^2+2\left(y-\frac{3}{2}\right)^2\right]-\frac{1}{4}\le-\frac{1}{4}\)(luôn âm)

1)=2x^2+(x-1)^2+1
Tổng 2 số không âm và 1 luôn dương
2)
Tồn tại A=> x khác +-1
A=(x+1)/(x-1)=1+2/(x-1)
x-1={-2,-1,1,2}
x={-1,0,2,3}


Vì \(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1\ge1>0\) với mọi giá trị của \(x\) nên giá trị của biểu thức luôn luôn âm với mọi giá trị khác 0 và khác -3 của \(x\)

\(a;x^2-3x+3=x^2-2\cdot\frac{3}{2}x+\frac{9}{4}-\frac{9}{4}+3\)
\(=\left(x-\frac{3}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\forall x\Leftrightarrow x^2-3x+3>0\forall x\)

Ta có: \(P=\frac{x^4+x^3+x+1}{x^4-x^3+2x^2-x+1}=\frac{x^3\left(x+1\right)+\left(x+1\right)}{x^4-x^3+x^2+x^2-x+1}=\frac{\left(x^3+1\right)\left(x+1\right)}{x^2\left(x^2-x+1\right)+\left(x^2-x+1\right)}\)
\(=\frac{\left(x+1\right)\left(x^2-x+1\right)\left(x+1\right)}{\left(x^2-x+1\right)\left(x^2+1\right)}=\frac{\left(x+1\right)^2\left(x^2-x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)}\)
Vì \(\hept{\begin{cases}x^2+1\ge1>0\\x^2-x+1=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\end{cases}}\)
Nên mẫu số luôn luôn khác 0
Do đó: \(P=\frac{\left(x+1\right)^2\left(x^2-x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)}=\frac{\left(x+1\right)^2}{x^2+1}\)
Vì \(\hept{\begin{cases}\left(x+1\right)^2\ge0\\x^2+1>0\end{cases}\left(\forall x\right)}\) nên \(P\ge0\left(\forall x\right)\)
\(P=\frac{x^4+x^2+x+1}{x^4-x^2+2x^2-x+1}=\frac{\left(x+1\right)^2\left(x^2-x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)}\)
Do \(\left(x^2+1\right)\left(x^2-x+1\right)\ne0\)do đó không cần điều kiện của x
Vậy \(P=\frac{\left(x+1\right)^2\left(x^2-x+1\right)}{\left(x^2+1\right)\left(x^2-x+1\right)}=\frac{\left(x+1\right)^2}{x^2+1}\)
\(\hept{\begin{cases}\left(x+1\right)^2\ge0\forall x\\x^2+1>0\forall x\end{cases}\Rightarrow P\ge0\forall x}\)

a. \(2x^2-4x+10=x^2-2x+1+x^2-2x+1+8=\left(x-1\right)^2+\left(x-1\right)^2+8=2\left(x-1\right)^2+8\)
Vì \(2\left(x-1\right)^2\ge0\Rightarrow2\left(x-1\right)^2+8\ge8\)
Vậy...
b. \(x^2+x+1=x^2+x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x+\frac{1}{2}\right)^2\ge0\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy..
c. \(2x^2-6x+5=x^2-4x+4+x^2-2x+1=\left(x-2\right)^2+\left(x-1\right)^2\)
Vì \(\hept{\begin{cases}\left(x-2\right)^2\ge0\\\left(x-1\right)^2\ge0\end{cases}}\Rightarrow\left(x-2\right)^2+\left(x-1\right)^2\ge0\)
Vậy...

a) Đặt \(A=x^2+4x+7\)
\(A=\left(x^2+4x+4\right)+3\)
\(A=\left(x+2\right)^2+3\)
Mà \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow A\ge3>0\)
b) Đặt \(B=4x^2-4x+5\)
\(B=\left(4x^2-4x+1\right)+4\)
\(B=\left(2x-1\right)^2+4\)
Mà \(\left(2x-1\right)^2\ge0\forall x\)
\(\Rightarrow B\ge4>0\)
c) Đặt \(C=x^2+2y^2+2xy-2y+3\)
\(C=\left(x^2+2xy+y^2\right)+\left(y^2-2y+1\right)+2\)
\(C=\left(x+y\right)^2+\left(y-1\right)^2+2\)
Mà \(\left(x+y\right)^2\ge0\forall x;y\)
\(\left(y-1\right)^2\ge0\forall y\)
\(\Rightarrow C\ge2>0\)