Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{P_nC_n^k}{n!A_n^k}=\frac{n!.\frac{n!}{k!\left(n-k\right)!}}{n!.\frac{n!}{\left(n-k\right)!}}=\frac{1}{k!}\)
Chắc là bạn ghi nhầm đề

gọi số cần tìm là abcdef (a#0 ; a;b;c;d;e;f € A ; f chẵn )
f có 3 cách chọn
a có 5 cách chọn lọc
b;c;d;e đều có 6 cách chọn
=> có 3*5*6*6*6*6 = 19440 số thỏa mãn yêu cầu bài toán
b) gọi số cần tìm là abcdef (a#0;f=0,5 ; a;b;c;d;e;f € A )
f=0,5 => f có 2 cách chọn
a có 5 cách chọn
b;c;d;e đều có 6 cách chọn
=> có 2*5*6*6*6*6 = 12960

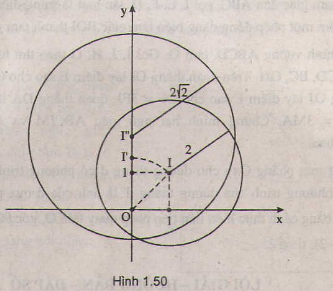
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)


Vì mỗi số hữu tỷ được viết dưới dạng phân số tối giản nên tử số và mẫu số không có ước nguyên tố chung nào.
Có 8 ước nguyên tố của 20! Là 2;3;5;7;11;13;17;19.
Mỗi một số nguyên tố này chỉ được chọn hoặc thuộc tử số hoặc mẫu số. Có tất cả 28 = 256 cách như vậy.
Tuy nhiên không phải tất cả 256 phân số này đều nhỏ hơn 1. Thật vậy; với mỗi phân số ta ghép cặp với phân số nghịch đảo của nó; có 128 cặp như thế; mà chỉ có 1 trong hai phân số đó nhỏ hơn 1.
Như vậy có tất cả 128 phân số thỏa mãn đầu bài.
Chọn B.