Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A E M B C H N S
Xét tam giác ABC có : \(BC=AB.\tan60^0=2a\sqrt{3}\Rightarrow S_{\Delta ABC}=2a^2\sqrt{3}\)
\(V_{S.ABCD}=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}a\sqrt{3}.2a^2\sqrt{3}=2a^3\)
- Gọi N là trung điểm cạnh SA. Do SB//(CMN) nên d(SB. CM)=d(SB,(CMN))
=d(B,(CMN))
=d(A,(CMN))
- Kẻ \(AE\perp MC,E\in MC\) và kẻ \(AH\perp NE,H\in NE\), ta chứng minh được \(AH\perp\left(CMN\right)\Rightarrow d\left(A,\left(CMN\right)\right)=AH\)
Tính \(AE=\frac{2S_{\Delta AMC}}{MC}\) trong đó :
\(S_{\Delta AMC}=\frac{1}{2}AM.AC.\sin\widehat{CAM}=\frac{1}{2}a.4a\frac{\sqrt{3}}{2}=a^2\sqrt{3};MC=a\sqrt{13}\)
\(\Rightarrow AE=\frac{2a\sqrt{3}}{\sqrt{13}}\)
Tính được \(AH=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(A,\left(CMN\right)\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(SB,CM\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\)

1.
\(V=\frac{1}{3}SA.\frac{1}{2}AB.BC=\frac{1}{6}.a.a.2a=\frac{a^3}{3}\)
2.
\(V=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}.2a\sqrt{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3}{2}\)
P/s: chóp này là chóp "có đáy là tam giác đều" chứ không phải "chóp tam giác đều"
Hai loại này khác xa nhau đấy, ko lộn xộn nhầm lẫn được đâu
3.
Câu này đề sai
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\Rightarrow\Delta SAC\) vuông tại A
\(\Rightarrow SC>SA\) (cạnh huyền luôn lớn hơn cạnh góc vuông)
Do đó đề cho \(SA=SC\) là vô lý
4.
\(AC=BD=\sqrt{AB^2+AD^2}=2a\)
\(\widehat{SCA}=60^0\Rightarrow SA=SC.tan60^0=2a\sqrt{3}\)
\(V=\frac{1}{3}SA.AB.AD=\frac{1}{3}.2a\sqrt{3}.a.a\sqrt{3}=2a^3\)

S A B M N C
Dùng định lý hàm số Cosin tính được \(MN=2a\sqrt{3}\)
\(AM=2a\sqrt{2},AN=2a\). Tam giác vuông SAC có SC=2SA nên góc ASC =60 độ suy ra tam giác AMN vuông tại A.
Gọi H là trung điểm của MN, vì SA=SM=SN và tam giác AMN vuông tại A \(\Rightarrow SH\perp\left(AMN\right)\), tính được SH=a
Tính được \(V_{S.AMN}=\frac{2\sqrt{2}a^3}{3}\)
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM.SN}{SB.SC}=\frac{1}{3}\) \(\Rightarrow V_{S.ABC}=2\sqrt{2}a^3\)
Vậy d(C;(SAB)) =\(\frac{3V_{S.ABC}}{S_{\Delta SAB}}=\frac{6a^3\sqrt{2}}{3a^2}=2a\sqrt{2}\)

A B C S H
Gọi H là trung điểm của BC=> HA=HB=HC
Kết hợp với giả thiết
SA=SB=SC=>\(SH\perp BC,\Delta SHA=\Delta SHB=SHC\)
\(\begin{cases}SH\perp\left(ABC\right)\\\widehat{SAH}=60^0\end{cases}\)
Tam giác ABC là tam giác vuông cân tại A
\(AC=AB=a\sqrt{2}\Rightarrow BC=2a\Rightarrow AH=a\)
Tam giác SHA vuông :
\(SH=AH.\tan60^0=a\sqrt{3}\Rightarrow V_{S.ABC}=\frac{1}{3}.\frac{1}{2}AB.AC.SH=\frac{\sqrt{3}a^3}{3}\)
Gọi O; R lần lượt là tâm và bán kính của mặt cầu ngoại tiếp chóp S.ABC. Suy ra P thuộc đường thẳng SH, nên O thuộc mặt phẳng (SBC). Do đó R là bán kính đường tròn ngoại tiếp tam giác SBC.
Xét tam giác SHA ta có : \(SA=\frac{SH}{\sin60^0}=2a\Rightarrow\Delta SBC\) là tam giác đều có độ dài cạnh bằng 2a.
Suy ra \(R=\frac{2a}{2\sin60^0}=\frac{2a\sqrt{3}}{3}\)

Đây là công thức tính thể tích tứ diện khi biết các cạnh bên và các góc đỉnh với \(SA=x\) ; \(SB=y\); \(SC=z\); \(\widehat{BSA}=\alpha;\widehat{BSC}=\beta;\widehat{CSA}=\gamma\)
\(\Rightarrow V=\frac{1}{6}xyz\sqrt{1+2cos\alpha.cos\beta.cos\gamma-cos^2\alpha-cos^2\beta-cos^2\gamma}\)
Bạn cứ lắp số liệu vào công thức là được
Chọn D.
Gọi là hình chiếu vuông góc của A lên mp (SBC) . Gọi I, K lần lượt là hình chiếu vuông góc của H lên SB và SC.
Ta có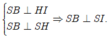
Chứng minh tương tự ta được SC ⊥ SK
∆ SAI = ∆ SAK (cạnh huyền – góc nhọn) => SI = SK
Khi đó ∆ SHI = ∆ SHK (cạnh huyền – cạnh góc vuông) => HI = HK. Do đó SH là đường phan giác trong của BSC, nên HSI = 30 °
Trong tam giác vuông SAI,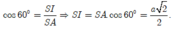
Trong tam giác vuông HIS,
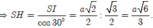
Khi đó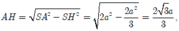

Vậy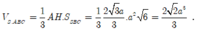
Cách 2: Sử dụng công thức tính nhanh
Nếu khối chóp S.ABC có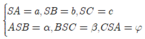 thì
thì
Áp dụng: Với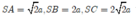
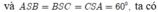
Trên các cạnh SB, SC lần lượt lấy các điểm B’, C’ sao cho SB' = SC' = SA = a 2
Khi đó chóp S.AB'C' là khối chóp tam giác đều. Đồng thời ASB = BSC = CSA = 60 ° nên AB' = B'C' = AC' = SA = a 2
Gọi H là hình chiếu của S lên mặt phẳng (AB'C'). Khi đó dễ dàng chứng minh được các tam giác SHA, SHB', SHC' bằng nhau. Suy ra HA, HB', HC' bằng nhau. Hay H là tâm đường tròn ngoại tiếp tam giác AB'C'. Vì tam giác AB'C' đều nên H cũng là trọng tâm tam giác AB'C'.
Ta có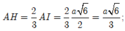
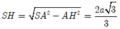
Ta có