Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

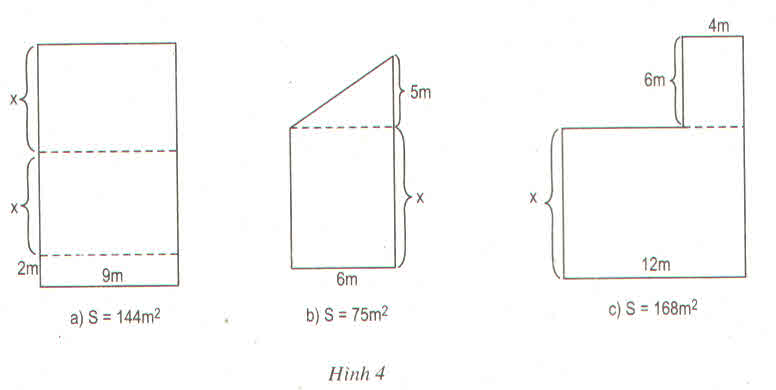
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.

c)(x2+x)2-2(x2+x)-15
đặt x2+x=a ta có
a2-2a-15
=a2+3a-5a-15
=(a2+3a)-(5a+15)
=a(a+3)-5(a+3)
=(a+3)(a-5)
thay a=x2+x
(x2+x+3)(x2+x-5)

\(P=14-\left(2x-5\right)^2\)
Vì: \(-\left(2x-5\right)^2\le0\)
=> \(14-\left(2x-5\right)^2\le14\)
Dấu bằng xảy ra khi \(2x-5=0\Leftrightarrow x=2,5\)
Vậy GTLN của P la 14 khi x=2,5

\(3f\left(x\right)+2f\left(1-x\right)=2x+9\)
\(\left\{\begin{matrix}3f\left(2\right)+2f\left(-1\right)=2.2+9=13\left(1\right)\\3f\left(-1\right)+2f\left(2\right)=2.\left(-1\right)+9=7\left(2\right)\end{matrix}\right.\)
Lấy (1) nhân 3 trừ đi (2) nhân 2:
\(\left(3.3-2.2\right)f\left(2\right)+\left(6-6\right)f\left(-1\right)=13.3-7.2\)
\(f\left(2\right)=\frac{39-14}{9-4}=\frac{25}{5}=5\)
Câu hỏi của Phạm Mai Chi - Toán lớp 8 - Học toán với OnlineMath

Diện tích đáy lăng trụ là:
\(S=\dfrac{1}{2}\cdot2x=x\left(cm^2\right)\)
\(V=S\cdot h\)
=>x=V/h=3(cm)

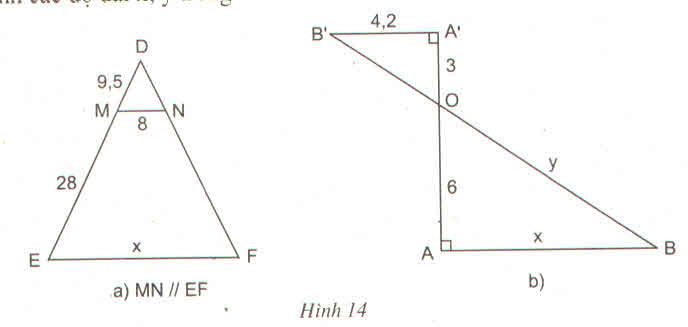
* Trong hình 14a
mà DE = MD + ME = 9.5 + 28 = 37.5

* Trong hình 14b
Ta có A’B’ ⊥ AA'(gt) và AB ⊥ AA'(gt)
=> A’B’ // AB =>


∆ABO vuông tại A
=> OB2 = y2 = OA2 + AB2
=> y2 = 62+ 8,42
=> y2 = 106,56
=> y ≈ 10,3

a, \(A=-x^2+2x+2\)
\(=-\left(x^2-2x-2\right)=-\left(x^2-2x+1-3\right)\)
\(=-\left(x-1\right)^2+3\le3\)
Dấu " = " khi \(-\left(x-1\right)^2=0\Leftrightarrow x=1\)
Vậy \(MAX_A=3\) khi x = 1
b, \(B=-x^2-8x+17\)
\(=-\left(x^2+8x-17\right)\)
\(=-\left(x^2+8x+16-33\right)\)
\(=-\left(x+4\right)^2+33\le33\)
Dấu " = " khi \(-\left(x+4\right)^4=0\Leftrightarrow x=-4\)
Vậy \(MAX_B=33\) khi x = -4
c, \(C=-x^2+7x+15\)
\(=-\left(x^2-\dfrac{7}{2}x.2+\dfrac{49}{4}-\dfrac{109}{4}\right)\)
\(=-\left(x-\dfrac{7}{2}\right)^2+\dfrac{109}{4}\le\dfrac{109}{4}\)
Dấu " = " khi \(-\left(x-\dfrac{7}{2}\right)^2=0\Leftrightarrow x=\dfrac{7}{2}\)
Vậy \(MAX_C=\dfrac{109}{4}\) khi \(x=\dfrac{7}{2}\)
d, \(D=-x^2-5x+11\)
\(=-\left(x^2+\dfrac{5}{2}.x.2+\dfrac{25}{4}-\dfrac{69}{4}\right)\)
\(=-\left(x+\dfrac{5}{2}\right)^2+\dfrac{69}{4}\le\dfrac{69}{4}\)
Dấu " = " khi \(-\left(x+\dfrac{5}{2}\right)^2=0\Leftrightarrow x=\dfrac{-5}{2}\)
Vậy \(MAX_D=\dfrac{69}{4}\) khi \(x=\dfrac{-5}{2}\)
f, sai đề à?
g, \(G=-x^2-x-y^2-3y+13\)
\(=-\left(x^2+x+y^2+3y-13\right)\)
\(=-\left(x^2+\dfrac{1}{2}x.2.+\dfrac{1}{4}+y^2+\dfrac{3}{2}.x.2+\dfrac{9}{4}-15,5\right)\)
\(=-\left(x+\dfrac{1}{2}\right)^2-\left(y+\dfrac{3}{2}\right)^2+15,5\le15,5\)
Dấu " = " khi \(\left\{{}\begin{matrix}-\left(x+\dfrac{1}{2}\right)^2=0\\-\left(y+\dfrac{3}{2}\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-1}{2}\\y=\dfrac{-3}{2}\end{matrix}\right.\)
Vậy \(MAX_G=15,5\) khi \(\left\{{}\begin{matrix}x=\dfrac{-1}{2}\\y=\dfrac{-3}{2}\end{matrix}\right.\)

a) x = 1
b) x = 6; x = -3
c) x = 5,5; x = 1,5
d) x = 1; x = -1
e) x = -2; x = -1,000000371....
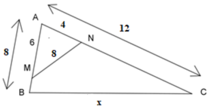


Ta có:
A N A B = 4 8 = 1 2 , A M A C = 6 12 = 1 2 ⇒ A N A B = A M A C = 1 2
Xét ΔANM và ΔABC có:
A N A B = A M A C (chứng minh trên)
A chung
⇒ ΔANM ~ ΔABC (c - g - c)
⇒ A N A B = A M A C = M N C B = 1 2
⇒ 8 x = 1 2 ⇒ x = 8.2 = 16
Đáp án: B