Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) các tứ giác ACC'A, BDD'B' là hình chữ nhật vì là các mặt bên của hình chữ nhật
b) ta có AC'2=AB2+AD2+AA'2 vì đó là công thức tính đường chéo của hình hộp chữ nhật đã được cm rồi
hoặc bạn có thể tham khảo cm trong sgk
c) diện tích toàn phần của hình hộp chữ nhật là
2*12*16+2*12*15+2*16*15=1224 cm2
thể tích của hình hộp chữ nhật là
12*16*15=2880 cm3

1a/IM vuông góc AB=>AMI=90 do
IN vuông góc AC=>ANI=90 do
△ABC vuông tại A=>BAC=90 do
=>góc AMI= gocANI= gocBAC= 90 do => tứ giác AMIN là hình chữ nhật
1b/Có I dx vs D qua N => ID là đường trung trực của AC=>AI=AD; IC=ID(1)
Trong △ABC có AI là đường trung tuyến ứng với cạnh huyền BC =>AI=1/2BC hay AI=IC(2)
Từ (1) va (2) => AI=IC=CD=DA => Tu giac AICD la hthoi
2a/ Có M là TĐ AB và M là điểm đối xứng giữa E và H
=> AM=MB VA EM=MH hay AB giao voi EH tai TD M
=> Tg AEBH la hbh co AHB=90 do => Hbh AEBH la hcn
2b/Co AEBH la hcn=>EH=AB
+) Mà AB=AC=>EH=AC(1)
+) △ABC cân tại A có AH là đường cao đồng thời phân giác của góc BAC => góc BAH=góc HAC.
Co goc BAH=1/2 EAH ; góc AHE=1/2AHB
Ma goc EAH= goc AHB=>BAH=AHE hay goc HAC= goc AHE.
Mà 2 góc này ở vị trí SLT=> EH//AC(2)
Từ (1) va (2)=>tg AEHC la hbh

Bài 1)
a) Tứ giác AIHK có 3 góc vuông \(\widehat{HKA}=\widehat{HIA}=\widehat{KAI}=90^0\)
Nên suy ra góc còn lại cũng vuông.Tứ giác có 4 góc vuông là hình chữ nhật
b) Câu này không đúng rồi bạn
Nếu thực sự hai tam giác kia đồng dạng thì đầu bài phải cho ABC vuông cân
Vì nếu góc AKI = góc ABC = 45 độ ( IK là đường chéo đồng thời là tia phân giác của hình chữ nhật)
c) Ta có : Theo hệ thức lượng trong tam giác ABC vuông
\(AB^2=BC.BH=13.4\)
\(\Rightarrow AB=2\sqrt{13}\)
\(AC=\sqrt{9\cdot13}=3\sqrt{13}\)
Vậy \(S_{ABC}=\frac{AB\cdot AC}{2}=\frac{6\cdot13}{2}=39\left(cm^2\right)\)
Bài 2)
a) \(ED=AD-AE=17-8=9\)
Xét tỉ lệ giữa hai cạnh góc vuông trong hai tam giác ABE và DEC ta thấy
\(\frac{AB}{AE}=\frac{ED}{DC}\Leftrightarrow\frac{6}{8}=\frac{9}{12}=\frac{3}{4}\)
Vậy \(\Delta ABE~\Delta DEC\)
b) \(\frac{S_{ABE}}{S_{DEC}}=\frac{AB\cdot AE\cdot\frac{1}{2}}{DE\cdot DC\cdot\frac{1}{2}}=\frac{6\cdot8}{9\cdot12}=\frac{4}{9}\)
c) Kẻ BK vuông góc DC.Suy ra tứ giác ABKD là hình chữ nhật vì có 4 góc vuông
Nên BK = AD và AB = DK
\(\Rightarrow KC=DC-DK=12-6=6\)
Theo định lý Pytago ta có
\(BC=\sqrt{BK^2+KC^2}=\sqrt{17^2+6^2}=5\sqrt{13}\)

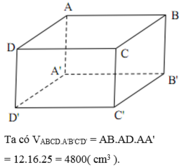
Diện tích xung quanh:
2 x 25 x (12+16)= 1400(cm2)
Diện tích 2 đáy:
2 x 12 x 16= 384(cm2)
Diện tích toàn phần:
1400+384= 1784(cm2)
Thể tích HHCN:
12 x 25 x 16= 4800(cm3)
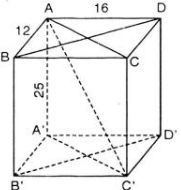



a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒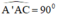
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )