Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp:
- Gắn hệ trục tọa độ Oxyz, tìm tọa độ các điểm E, M.
- Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin α = n → . u → n → . u →
Cách giải:
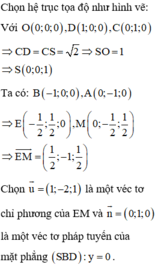
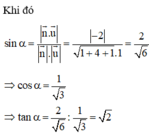

Đáp án A
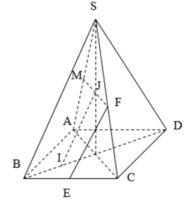
Gọi I,J lần lượt là trung điểm cạnh BC và SA
Ta có A C ⊥ S B D , EI // AC, MJ//AC => E I ⊥ ( S B D ) , M J ⊥ ( S B D )
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
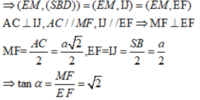

Đáp án B
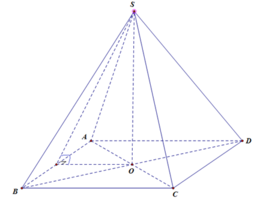
Ta có
S A B , A B C D ^ = S H O ^ = α ⇒ O H = h tan α ⇒ A D = 2 h tan α
Thể tích khối chóp S . A B C D là
V S . A B C D = 1 3 . S A B C D . h = 1 3 2 h tan α 2 . h = 4 h 3 3 tan 2 α

Chọn C.
Phương pháp:
Thể tích của khối chóp ngoại tiếp hình chóp

Cách giải:
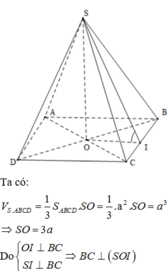
Gọi O là tâm của hình vuông ABCD, I là trung điểm của BC.
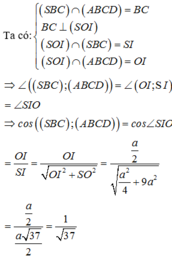

Đáp án A

Gọi I,J lần lượt là trung điểm cạnh BC và SA
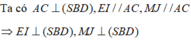
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
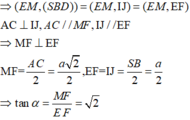

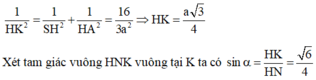
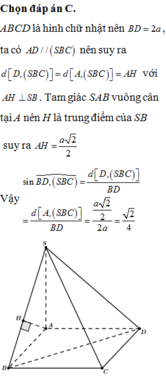

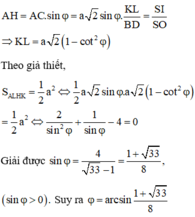
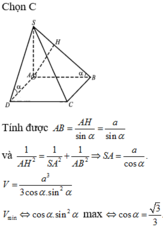
Đáp án C
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì: