Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ dàng chứng minh MN // BC
Xét \(\Delta SBC\) có MN // BC và MN đi qua trọng tâm G
\(\Rightarrow\) \(\begin{cases}SM=\frac{2}{3}SB\\SN=\frac{2}{3}SC\end{cases}\)
Sử dụng công thức tỉ lệ thể tích đố với 2 khối tứ diện S.AMN và S.ABC ta có
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=1.\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\\ \Rightarrow V_{S.AMN}=\frac{4}{9}.V_{S.ABC}\)
Tính được \(V_{S.ABC}=\frac{1}{6}SA.AB.BC=\frac{a^3}{6}\)
\(\Rightarrow V_{S.AMN}=\frac{2a^3}{27}\)

Kẻ SH vuông góc với BC tại H => SH vuông góc với (ABC)
Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N
Ta có góc SMH = góc SNH = 60 độ
Dễ thấy tam giác SHM = tam giác SHN => HM = HN
Ta có HM = HB.sin 30 = 1/2 HB hay HB = 2 HM
HN = HC.sin 60 = HC.căn 3 /2 => HC = 2/căn 3.HN = 2/căn 3 .HM
=> BC = a = HB + HC = ( 2 + 2/căn 3).HM
=> HM = a/(2 + 2/căn 3) = a.căn 3 /(2+ 2.căn 3)
=> SH = HM.tan 60 = 3a/(2+2.căn 3)
Có AB = BC/2 = a/2
AC = BC.căn 3/2 = a.căn 3/2
S(ABC) = 1/2.AB.AC = 1/8.a^2.căn 3
=> V(SABC) = 1/3.3a/(2+2.căn 3) . 1/8.a^2.căn 3 = a^3.căn 3 /[16.(1+ căn 3)]

A B C S H
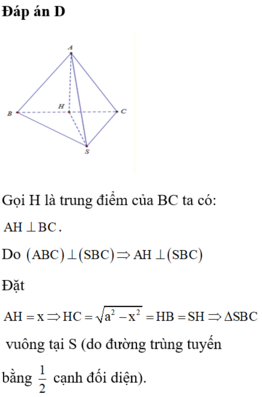
Gọi H là trung điểm của BC=> HA=HB=HC
Kết hợp với giả thiết
SA=SB=SC=>\(SH\perp BC,\Delta SHA=\Delta SHB=SHC\)
\(\begin{cases}SH\perp\left(ABC\right)\\\widehat{SAH}=60^0\end{cases}\)
Tam giác ABC là tam giác vuông cân tại A
\(AC=AB=a\sqrt{2}\Rightarrow BC=2a\Rightarrow AH=a\)
Tam giác SHA vuông :
\(SH=AH.\tan60^0=a\sqrt{3}\Rightarrow V_{S.ABC}=\frac{1}{3}.\frac{1}{2}AB.AC.SH=\frac{\sqrt{3}a^3}{3}\)
Gọi O; R lần lượt là tâm và bán kính của mặt cầu ngoại tiếp chóp S.ABC. Suy ra P thuộc đường thẳng SH, nên O thuộc mặt phẳng (SBC). Do đó R là bán kính đường tròn ngoại tiếp tam giác SBC.
Xét tam giác SHA ta có : \(SA=\frac{SH}{\sin60^0}=2a\Rightarrow\Delta SBC\) là tam giác đều có độ dài cạnh bằng 2a.
Suy ra \(R=\frac{2a}{2\sin60^0}=\frac{2a\sqrt{3}}{3}\)

A B C D H K S
Hạ \(SH\perp BC\Rightarrow\left(SBC\right)\perp\left(ABC\right)\)
\(\Rightarrow SH\perp BC;SH=SB.\sin\widehat{SBC}=a\sqrt{3}\)
Diện tích : \(S_{ABC}=\frac{12}{\boxtimes}BA.BC=6a^2\)
Thể tích : \(V_{s.ABC}=\frac{1}{3}S_{ABC}.SH=2a^3\sqrt{3}\)
Hạ \(HD\perp AC\left(D\in AC\right),HK\perp SD\left(K\in SD\right)\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H,\left(SAC\right)\right)\)
\(BH=SB.\cos\widehat{SBC}=3a\Rightarrow BC=4HC\)
\(\Rightarrow d\left(B,\left(SAC\right)\right)=4d\left(H,SAC\right)\)
Ta có : \(AC=\sqrt{BA^2+BC^2}=5a;HC=BC-BH=a\)
\(\Rightarrow HD=BA.\frac{HC}{AC}=\frac{3a}{5}\)
\(HK=\frac{SH.HS}{\sqrt{SH^2+HD^2}}=\frac{3a\sqrt{7}}{14}\)
Vậy \(d\left(B,\left(SAC\right)\right)=4HK=\frac{6a\sqrt{7}}{7}\)

Lời giải:
Gọi $H$ là chân đường cao kẻ từ $S$ xuống mặt phẳng $(ABC)$
Ta có \(\left\{\begin{matrix} SH\perp AB\\ SA\perp AB\end{matrix}\right.\Rightarrow AB\perp (SHA)\rightarrow AB\perp HA\)
Tương tự \(BC\perp HC\). Kết hợp với \(ABC\) vuông cân tại $B$ suy ra \(ABCH\) là hình vuông
Có \(AH\parallel (SBC)\Rightarrow d(A,(SBC))=d(H,(SBC))\)
Kẻ \(HT\perp SC\). Có \(\left\{\begin{matrix} SH\perp BC\\ HC\perp BC\end{matrix}\right.\Rightarrow BC\perp (SHC)\Rightarrow BC\perp HT\)
Do đó \(HT\perp (SBC)\Rightarrow d(H,(SBC))=HT=\sqrt{\frac{SH^2.HC^2}{SH^2+HC^2}}=\sqrt{\frac{SH^2.AB^2}{SH^2+AB^2}}=\sqrt{2}\Rightarrow SH=\sqrt{6}a\)
Từ trung điểm $O$ của $AC$ dựng trục vuông góc với mặt phẳng $(ABC)$. Trên trục đó ta lấy điểm $I$ là tâm mặt cầu ngoại tiếp.
\(IS^2=IA^2=IH^2\Leftrightarrow (\overrightarrow{IO}+\overrightarrow{OH}+\overrightarrow{HS})^2=IO^2+OH^2\)
\(\Leftrightarrow HS^2+2\overrightarrow{IO}.\overrightarrow{HS}=0\)
Do \(\overrightarrow {SH}\parallel \overrightarrow {IO}\Rightarrow \overrightarrow {IO}=k\overrightarrow{SH}\). Thay vào PT trên có $k=\frac{1}{2}$
\(\Rightarrow IO=\frac{\sqrt{6}a}{2}\Rightarrow IA=\sqrt{IO^2+AO^2}=\sqrt{3}a\)
\(\Rightarrow S_{\text{mặt cầu}}=4\pi R^2=12a^2\pi\)

+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)