Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
S o B H A D G d H' C K
Câu a bạn tự tính nhé!
Câu b: Qua G kẻ đường thẳng d // CD , khoảng cách từ \(d\left(G;\left(SAB\right)\right)=d\left(d;\left(SAD\right)\right)\)
Kẻ HH' vuông CD , nối SH'. Lúc này SH' cách d tại K . \(d\left(K;\left(SAB\right)\right)\) là khoảng cách cần tìm.
Ta có: SH'AB =\(\frac{1}{2}S_{ABCD}\)=\(\frac{1}{2}\times2\sqrt{3}a^2=\sqrt{3}a^2\) \(\Rightarrow HH'=\frac{\sqrt{3}a^2}{a}=\sqrt{3}a\)
Vì K nằm trên d nên \(d\left(K;\left(SAB\right)\right)=\frac{2}{3}HH'=\frac{2\sqrt{3}a}{3}\)
\(\left(1-\dfrac{1}{2}\right)\):\(\left(1-\dfrac{1}{3}\right)\):\(\left(1-\dfrac{1}{4}\right)\):\(\left(1-\dfrac{1}{5}\right)\):\(\left(1-\dfrac{1}{6}\right)\):\(\left(1-\dfrac{1}{7}\right)\)
=\(\left(\dfrac{2-1}{2}\right)\):\(\left(\dfrac{3-1}{3}\right)\):\(\left(\dfrac{4-1}{4}\right)\):\(\left(\dfrac{5-1}{5}\right)\):\(\left(\dfrac{6-1}{6}\right)\)
=\(\dfrac{1}{2}\):\(\dfrac{2}{3}\):\(\dfrac{3}{4}\):\(\dfrac{4}{5}\):\(\dfrac{5}{6}\)
=\(\dfrac{1.\left(3.4.5\right)6}{\left(3.4.5\right)\left(2.2\right)}\)
=\(\dfrac{6}{2.2}=\dfrac{3}{2}\)
Chọn đáp án B
Gọi M là trung điểm BC.
Ta có: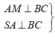 
Suy ra góc giữa (SBC) và (ABC) bằng góc S M A ^
Tam giác ABC vuông cân tại A:
Xét tam giác SAM vuông tại A có SA = AM = a
=>Tam giác SAM vuông cân tại A => S M A ^ = 45 °
a) Do B, C, D, E cách đều A và F nên chúng đồng phẳng (cùng thuộc mặt phẳng trung trực của AF).
Tương tự, A, B, F, D đồng phẳng và A, C, F, E đồng phẳng
Gọi I là giao của (AF) với (BCDE). Khi đó B, I, D là những điểm chung của hai mặt phẳng (BCDE) và (ABFD) nên chúng thẳng hàng. Tương tự, E, I , C thẳng hàng.
Vậy AF, BD, CE đồng quy tại I.
Vì BCDE là hình thoi nên BD vuông góc với BC và cắt BC tại I là trung điểm của mỗi đường. I là trung điểm của AF và AF vuông góc với BD và EC, do đó các đoạn thẳng AF, BD, và CE đôi một vuông góc với nhau cắt nhau tại trung điểm của chúng.
b) Do AI vuông góc (BCDE) và AB = AC =AD = AE nên IB = IC= ID = IE. Từ đó suy ra hình thoi BCDE là hình vuông. Tương tự, ABFD, AEFC là những hình vuông
) Gọi P là tr/điểm AS
=> SA v/góc BP (t/giác SAB đêu)
SA v/góc BM =>SA v/góc (BPM)
Gọi P, Q lần lượt là tr/điểm AS và AJ
=> PQ là đ/t/bình t/giác ASJ
=> SJ // PQ. Mặt khác, t/giác SAJ có:
vuông tại S
=> AS v/góc SJ => AS v/góc PQ
Lại có: AS v/góc BP (t/giác SAB đều) => AS v/góc (BPQ) => AS v/góc BQ, lúc đó M là giao điểm BQ và CD.
AB // JM => . Trong t/giác vuông ADM có:
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, góc BAD=120. Mặt bên (SAB) có SA=a, SB= a\(\sqrt{3}\) và vuông góc với mặt phẳng đáy. Gọi G là trọng tâm tam giác SCD. Tính thể tích hình chóp SABCD và khoảng cách từ G đến mặt phẳng (SAB). 
