Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

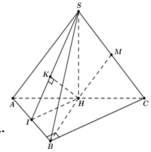
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Đáp án D
Phương pháp:
+ Tìm tâm và bán kính của mặt cầu
+ Xác định vị trí tương đối của mặt phẳng và mặt cầu để suy ra vị trí của điểm M
+ Tìm tọa độ của đường thẳng và mặt cầu thì ta giải hệ phương trình gồm phương trình đường thẳng và phương trình mặt cầu
Cách giải:
Mặt cầu (S) có tâm
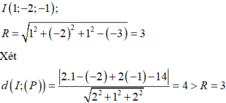
nên mặt phẳng (P) không cắt mặt cầu (S).Khi đó điểm M thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất thì M là giao điểm của đường thẳng d đi qua I , nhận n P → = 2 ; - 1 ; 2 làm VTCP với mặt cầu.
Phương trình đường thẳng
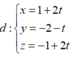
Tọa độ giao điểm của đường thẳng d và mặt cầu (S) thỏa mãn hệ phương trình
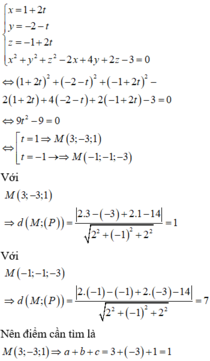

Đáp án B
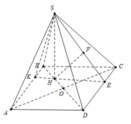
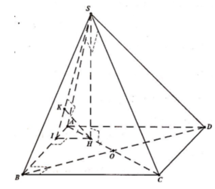
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14

Mặt cầu (S) có tâm I(-1;2;-3), R = 5. Nhận thấy A 2 ; 2 ; 1 ∈ S . Do đó (S) là mặt cầu ngoại tiếp tứ diện vuông ABCD. Gọi G là trọng tâm tam giác BCD ta có

![]()
![]()
Vì vậy

Chọn đáp án D.
Dấu bằng xảy ra khi và chỉ khi I G ⊥ B C D ⇔ B C D : 3 x + 4 z + 20 = 0 .
Chọn đáp án D.





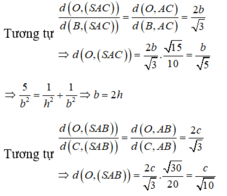
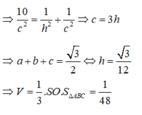
Đáp án D
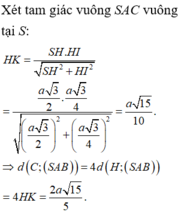
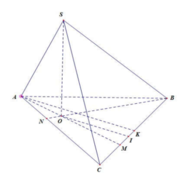
Gọi M, N lần lượt thuộc cạnh SB,SC sao cho S M = S N = 2.
Tam giác SMN đều ⇒ S M = S N = M N = 2.
Tam giác SAM có AS M ^ = 45 ∘ ⇒ A M = 2 2 − 2 .
Tam giác SAN vuông cân tại S ⇒ A N = S A 2 = 2 2 .
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ S I ⊥ A M N .
Tính bán kính đường tròn ngoại tiếp Δ A M N . Diện tích tam giác AMN là
S = p p − A M p − A N p − M N ⇒ R Δ A M N = A M . A N . M N 4 S = 2 4 − 2 2 S Δ A M N ,
với p = A M + A N + M N 2 .
Tam giác SAI vuông tại I, có S I = S A 2 − I A 2 = 4 − R 2 Δ A M N .
Ta có V S . A M N V S . A B C = S M S B . S N S C = 2 3 . 2 4 = 1 3 ⇒ V S . A B C = 3 V S . A M N ⇒ d B ; S A C = 9 V S . A M N S Δ S A C = 3 2 .