PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
5
4 tháng 5 2017
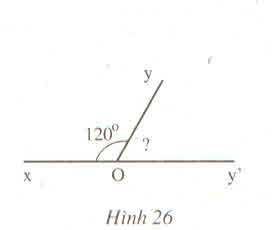
ta có : xOy va yOy' la hai goc ke nhau
=) xOy = 180 do
=> yOy' + xOy = xOy'
=> yOy' = xOy' - xOy =180 - 120 = 60 do
vay yOy' = 60 do
11 tháng 2 2018
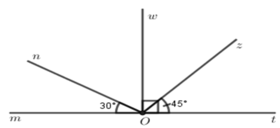
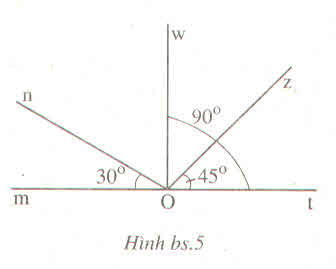
a)Các cặp góc kề nhau đỉnh O là: mOn và nOw; mOn và nOz; mOn và nOt; mOw và zOw; mOw và tOw; mOz và zOt; wOn và zOw; wOn và tOw; wOz và zOt.
b)góc mOt=180o; góc mOw=90o; nOw=60o;wOz=45o
c)mOn và nOw; wOz và zOt.
d)mOn và nOt ;wOm và wOt; mOz và zOt.
e)mOn và nOt; wOm và wOt; mOz và zOt.
TN
26 tháng 4 2017
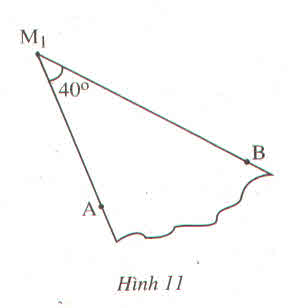
a, lấy BC-BD thì sẽ ra DC thôi
b,lấy góc BAD + DAC
C, THÌ có mỗi ABD và ADC kề nhau và kề bù trong hình vẽ thôi
Q
7 tháng 7 2017
3/ Chu vi hình chữ nhật:
\(\left(\dfrac{1}{4}+\dfrac{3}{10}\right)\cdot2=\dfrac{11}{10}\) (chưa biết đơn vị)
Diện tích hình chữ nhật:
\(\dfrac{1}{4}\cdot\dfrac{3}{10}=\dfrac{11}{20}\) (chưa biết đơn vị)
3 tháng 4 2017
Ta có : \(\dfrac{1}{2}xOy=\dfrac{1}{7}yOz\Rightarrow xOy=\dfrac{1}{7}yOz:\dfrac{1}{2}=\dfrac{2}{7}yOz\)
Ta lại có : góc xOy + góc yOz = 180 độ( hai góc kề bù )
\(\Rightarrow\) \(\dfrac{2}{7}yOz\) + góc yOz = 180 độ
\(\Rightarrow\)yOz(\(\dfrac{2}{7}+1\)) = 180 độ
\(\Rightarrow\)\(\dfrac{9}{7}yOz\)= 180 độ
\(\Rightarrow\)yOz = 180 : \(\dfrac{9}{7}\)=180 .\(\dfrac{7}{9}\)= 140 độ
Khi đó : xOy = 140 . \(\dfrac{2}{7}\)= 40 độ
23 tháng 10 2017
Chứng Minh:C=\(3^0+3^2+3^4+...+3^{2002}⋮7\)
Nhân C với \(3^2\)ta có:
\(9S=3^2+3^4+3^6+...+3^{2004}\)
\(\Rightarrow9S-S=\left(3^2+3^4+...+3^{2004}\right)-\left(3^0+3^2+3^4+...+3^{2002}\right)\)
\(\Rightarrow8S=3^{2004}-1\)
\(\Rightarrow S=\dfrac{3^{2004}-1}{8}\)
Chứng minh:
Ta có:\(3^{2004}-1=\left(3^6\right)^{334-1}=\left(3^6-1\right).a=7.104.a\)
\(\)UCLN(7;8)=1
\(\Rightarrow S⋮7\)
23 tháng 10 2017
Sửa lại 1 chút!
Chứng minh: C= \(3^0+3^2+3^4+3^6+...+3^{2002}\) chia hết cho 7
20 tháng 4 2017
Hop so be nhat la 4
Ta co: 2015=4+4+4+...+4+15 (500 so 4)
Vi 4 va 15 la hop so
Vay co tat ca 501 cach viet
Tick cho minh nhe
20 tháng 4 2017
Hợp số bé nhất là 4
> Ta có:2015=4+4+4+....+4+15( có tất cả 500 số 4)
Vì ta thấy 4 và 15 là hợp số
vậy nên suy ra ta sẽ có tất cả 501 cách viết
Tick mink nhé @Trịnh Minh Thành
m O n ^ v à n O t ^ ; m O w ^ v à w O t ^ ; m O z ^ v à z O t ^