Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k
Đặt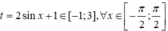 
phương trình trở thành f(t)=f(m)(1)
Với mỗi t ∈ - 1 ; 3 cho ta duy nhất một nghiệm x ∈ - π 2 ; π 2
Vậy ta cần tìm m để (1) có đúng ba nghiệm 
Chọn đáp án B.
Có 
Đặt t=f(x)+m bất phương trình trở thành: 
Vậy 
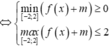
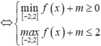
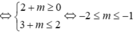
Chọn đáp án B.
Ta có:
\(f\left(1\right).f\left(-1\right)=\left(a+b\right).\left(-a+b\right)\)
\(\Rightarrow\left(a+b\right)\left(-a+b\right)=\left(a+b\right)^2\)
\(\Rightarrow-a+b=a+b\)
\(\Rightarrow a=-a\)
\(a\ne0\) thì làm sao có a thỏa mãn được?
Trần Thùy Dung ko biết thì đừng có làm. 5 - 3a - 3b = 5. Bài này trong violympic.
Bất phương trình m > f(x) - ln(-x) đúng với mọi x ∈ - 1 ; - 1 e
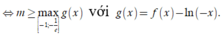
Ta có 
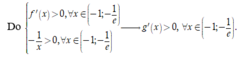
Suy ra hàm số g(x) đồng biến trên 
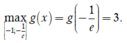
Chọn D.
