Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) 2x+y=4⇔y=−2x+4⇔x=12−y+22x+y=4⇔y=−2x+4⇔x=12−y+2. Do đó phương trình có nghiệm dạng tổng quát như sau:
{x∈Ry=−2x+4{x∈Ry=−2x+4 hoặc {x=−12x+2y∈R{x=−12x+2y∈R
b) Vẽ (d1): 2x + y = 4
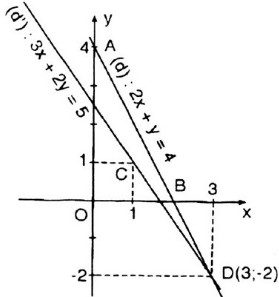
- Cho x = 0 => y = 4 được A(0; 4).
- Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): 3x + 2y = 5
- Cho x = 0 => y = 
được C(0; ).
- Cho y = 0 => x = 
được D(; 0).
Hai đường thẳng cắt nhau tại M(3; -2).
Thay x = 3, y = -2 vào từng phương trình ta được:
2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.
a) + Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔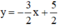 
Vậy phương trình (2) có nghiệm tổng quát là :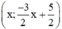 
(x ∈ R).
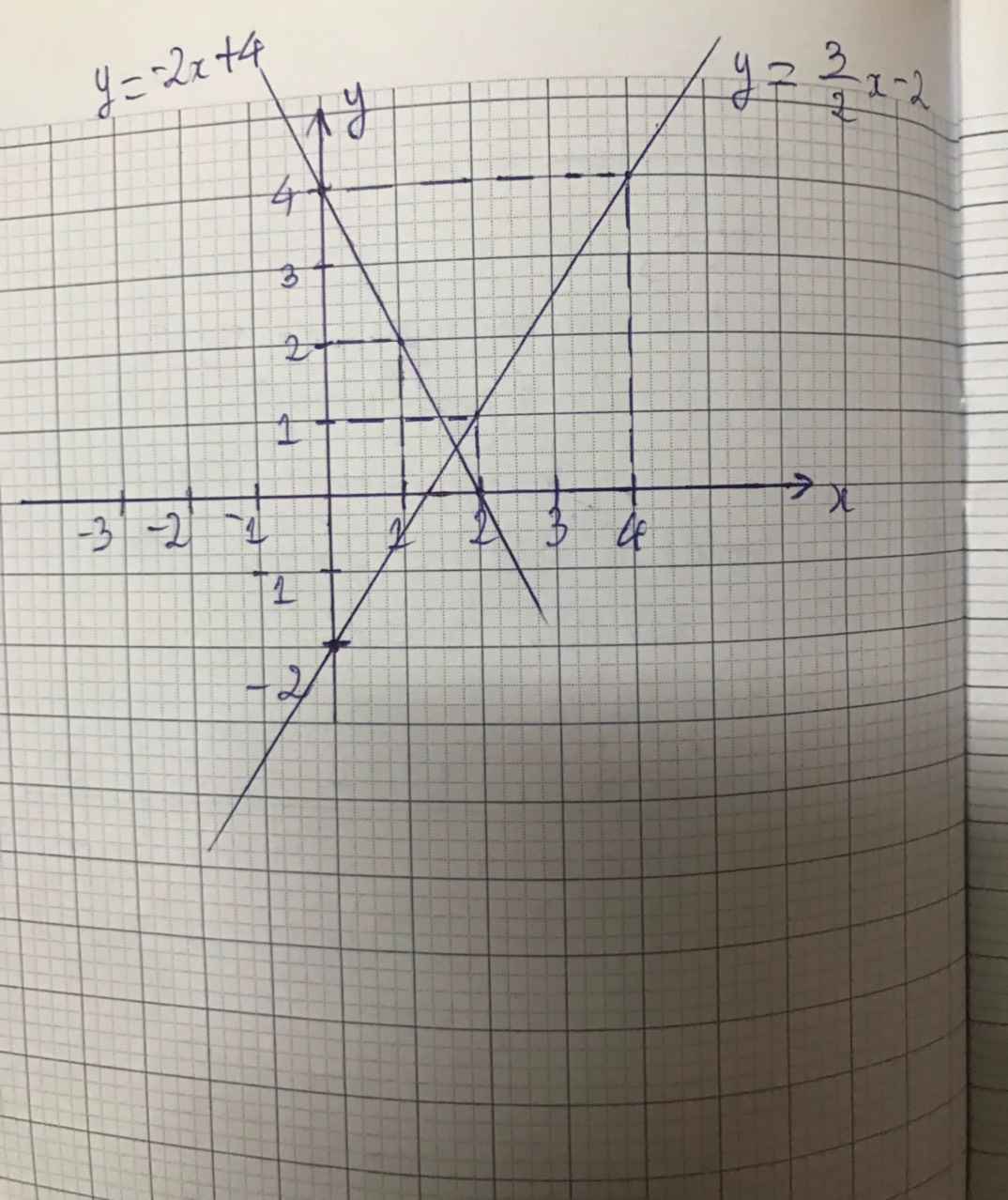
b) Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) :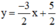 
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒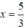 
⇒ (d’) đi qua hai điểm (0; 2,5) và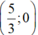 
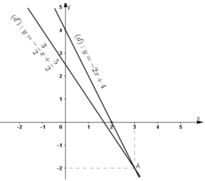
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2).
Bài 1 :
a) \(x^3-x^2-x-2=0\)
\(\Leftrightarrow x^3-2x^2+x^2-2x+x-2=0\)
\(\Leftrightarrow\left(x^3-2x^2\right)+\left(x^2-2x\right)+\left(x-2\right)=0\)
\(\Leftrightarrow x^2\left(x-2\right)+x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+x+1\right)=0\)(1)
Vì \(x^2+x+1=x^2+2.\frac{1}{2}.x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x+\frac{1}{2}\right)^2\ge0\forall x\)\(\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\forall x\)
\(\Rightarrow x^2+x+1\ge\frac{3}{4}\forall x\)(2)
Từ (1) và (2) \(\Rightarrow x-2=0\)\(\Leftrightarrow x=2\)
Vậy \(x=2\)
Bài 2:
\(2x^2+y^2-2xy+2y-6x+5=0\)
\(\Leftrightarrow x^2-2xy+y^2-2x+2y+1+x^2-4x+4=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)-\left(2x-2y\right)+1+\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(x-y\right)^2-2\left(x-y\right)+1+\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-y-1\right)^2+\left(x-2\right)^2=0\)(1)
Vì \(\left(x-y-1\right)^2\ge0\forall x,y\); \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-y-1\right)^2+\left(x-2\right)^2\ge0\forall x,y\)(2)
Từ (1) và (2) \(\Rightarrow\left(x-y-1\right)^2+\left(x-y\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x-y-1=0\\x-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=x-1\\x=2\end{cases}}\Leftrightarrow\hept{\begin{cases}y=1\\x=2\end{cases}}\)
Vậy \(x=2\)và \(y=1\)
Để pt có nghiệm khi duy nhất khi \(\frac{1}{2}\ne-\frac{2}{1}\)* luôn đúng *
Ta có : \(\hept{\begin{cases}x-2y=m+3\\2x+y=2m+1\end{cases}\Leftrightarrow\hept{\begin{cases}2x-4y=2m+6\\2x+y=2m+1\end{cases}}\Leftrightarrow\hept{\begin{cases}-5y=5\\x-2y=m+3\end{cases}\Leftrightarrow}\hept{\begin{cases}y=-1\\x=m+1\end{cases}}}\)
Thay vào biểu thức trên ta có : \(3x+2y>3\Rightarrow3\left(m+1\right)-2>3\)
\(\Leftrightarrow3m+3-2>3\Leftrightarrow3m>2\Leftrightarrow m>\frac{2}{3}\)
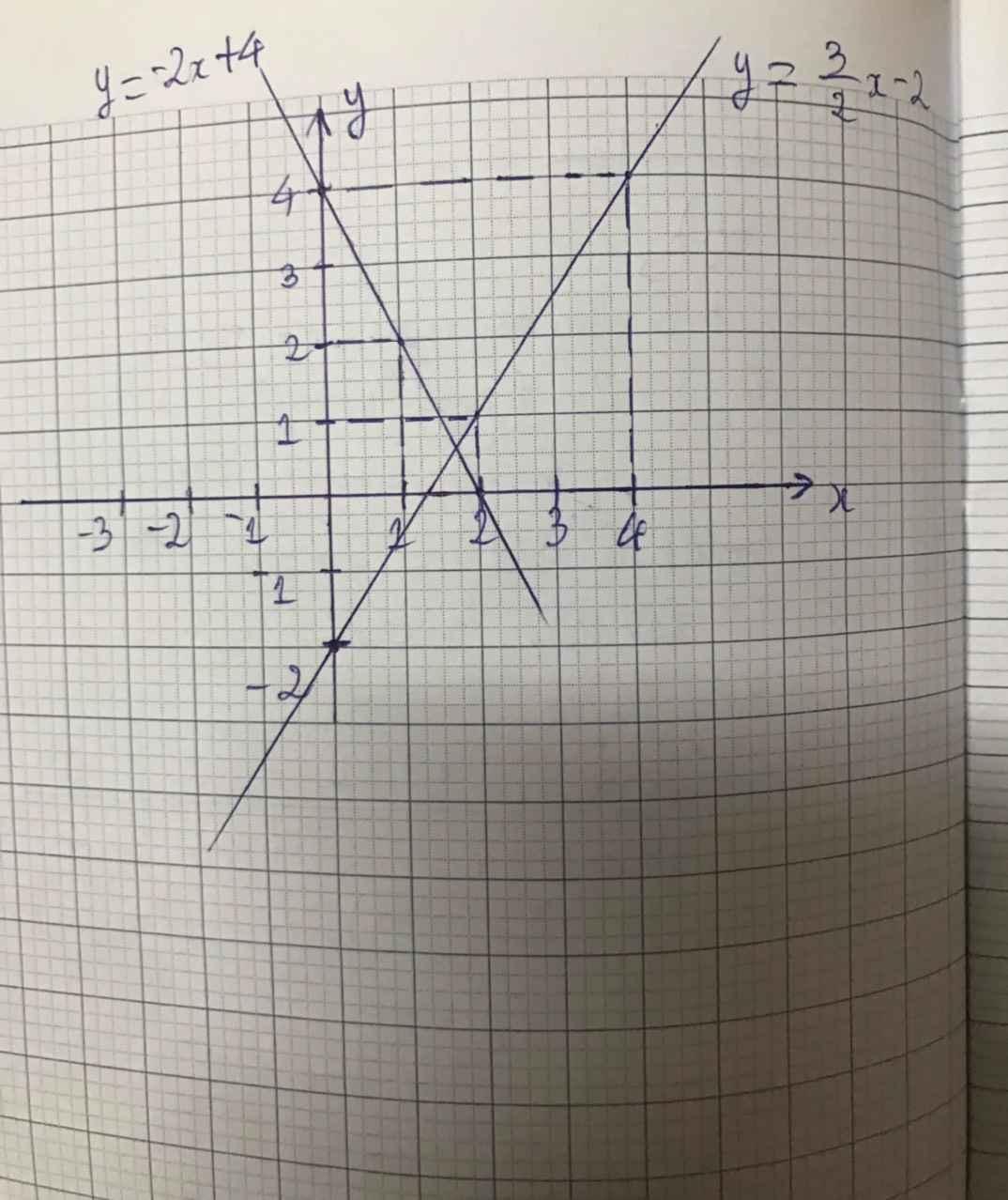
+ Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔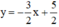
Vậy phương trình (2) có nghiệm tổng quát là :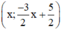
(x ∈ R).