
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

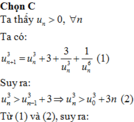
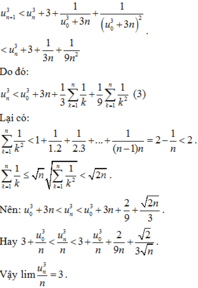

Chọn A
Phương pháp: Tìm công thức số hạng tổng quát
Cách giải: Ta có:
u ( 1 ) = 1
u ( 2 ) = u ( 1 ) + u ( 1 ) = 2 u ( 1 ) + 1
u ( 3 ) = u ( 2 ) + u ( 1 ) = 3 u ( 1 ) + 1 + 2
u ( 4 ) = u ( 3 ) + u ( 1 ) = 4 u ( 1 ) + 1 + 2 + 3
. . .
u ( 2017 ) = u ( 2016 ) + u ( 1 ) = 2017 u ( 1 ) + 1 + 2 + 3 . . . + 2016
⇒ u ( 2017 ) = 1 + 2 + 3 . . . + 2016 + 2017 = 2035153

\(u_n^2+2011=2u_n.u_{n+1}\Rightarrow u_{n+1}=\frac{u_n^2+2011}{2u_n}\)
Ta có \(u_1>0\), giả sử \(u_k>0\Rightarrow u_{k+1}=\frac{u_k^2+2011}{2u_k}>0\)
\(\Rightarrow\) Dãy đã cho là dãy dương
Mặt khác \(u_{n+1}=\frac{1}{2}\left(u_n+\frac{2011}{u_n}\right)\ge\frac{1}{2}.2\sqrt{2011}=\sqrt{2011}\)
\(\Rightarrow u_n\ge2011\) \(\forall n\ge1\Rightarrow\) dãy đã cho bị chặn dưới
Xét \(\frac{u_{n+1}}{u_n}=\frac{u_n^2+2011}{2u^2_n}=\frac{1}{2}+\frac{2011}{2u_n^2}\le\frac{1}{2}+\frac{2011}{2.2011}=1\) (do \(u_n\ge\sqrt{2011}\))
\(\Rightarrow u_{n+1}\le u_n\) \(\Rightarrow\) dãy đã cho là dãy giảm
Dãy giảm, bị chặn dưới \(\Rightarrow\) dãy có giới hạn
Gọi giới hạn của dãy là \(a\Rightarrow\sqrt{2011}\le a\le u_1\)
\(\Rightarrow a^2-2a^2+2011=0\)
\(\Rightarrow a^2=2011\Rightarrow a=\sqrt{2011}\)
\(\Rightarrow lim\left(u_n\right)=\sqrt{2011}\)