Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)

Câu 1.
A = {15;16;17;18;19} (0,25đ)
Câu 2.
a. 2.(72 – 2.32) – 60
= 2.(49 – 2.9) – 60 (0,25đ)
= 2.31 – 60 (0,25đ)
= 62 – 60 = 2 (0,25đ)
b. 27.63 + 27.37
= 27.(63 + 37) (0,25đ)
= 27.100 (0,25đ)
= 2700 (0,25đ)
c. l-7l + (-8) + l-11l + 2
= 7 + (-8) + 11 + 2 (0,5 đ)
= 12 (0,25đ)
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
= 568 – 34 {5.[9-9] + 10} (0,25đ)
= 568 – 34.10
= 568 – 340 (0,25đ)
= 228 (0,25đ)
Câu 3.
a)2x + 3 = 52 : 5
2x + 3 =5 (0,25đ)
2x = 5-3 (0,25đ)
2x =2 (0,25đ)
x=1 (0,25đ)
b)
105 – ( x + 7) = 27 : 25
105 – ( x + 7) = 22 (0,25đ)
105 – ( x + 7) = 4 (0,25đ)
x + 7 = 105 – 4 (0,25đ)
x + 7 = 101 (0,25đ)
x = 101 – 7 (0,25đ)
x = 94 (0,25đ)
Câu 4.
Gọi x (hs) là số học sinh lớp 6B phải tìm (30<x< 38, x)
Vì hs lớp 6B xếp 2, hàng, 4 hàng, 8 hàng đều vừa đủ nên x⋮2; x⋮4; x⋮8 hay x ∈ BC{2;4;8} (0,25đ)
Ta có: BCNN(2,4,8) = 8 (0,25đ)
⇒ BC(2,4,8) = B(8) ={0; 8; 16;24; 32; 40; …}
Mặt khác: 30<x< 38 (0,25đ)
Nên x = 32
Vậy số học sinh lớp 6B là 32 học sinh (0,25đ)
Câu 5.
Khi M nằm giữa và cách đều hai điểm A và B (0,5đ)
Vẽ được hình có điểm M là trung điểm của AB (0,5đ)
Câu 6.a)

0,25đ
Điểm A nằm giữa O và B (0,25đ)
Vì OA < OB ( 4 < 8 ) (0,25đ)
Ta có: AO + AB = OB
3 + AB = 6 (0,25đ)
AB = 6 -3 = 3 cm (0,25đ)
Vậy OA = AB = 3 cm (0,25đ)
b)
Vì A nằm giữa O, B và cách đều O và B ( OA = AB ) (0,25đ)
Nên A là trung điểm OB (0,25đ)

bn tính máy tính ý phần a bn để 2 1^2 làm phân số là bằng 5^2 rùi bn thực hiện phép tính nhé
PHần b thi bn để 0,5 và 0,75 làm phân số rùi tính là ra thui ak
nếu cần giải ra thi bảo mk mk giải cho nhé nhưng làm như trên đc mà nhỉ
a, (3^4.x +5^2).2^3=1^8
3^4.x+5^2=1^8: 2^3
3^4.x+5^2=3^16
rùi bn tính ra nhé
b, 1^3x-0,5x=0,75
x.(1^3-0,5)=0,75
rùi bn đổi ra như mk bảo là đc nhé

P = 7 + 72 + 73 + ... + 72016
=> P = 7( 1 + 7 + 72 + 73) + ... + 72013( 1 + 7 + 72 + 73)
=> P = 7( 1 + 7 + 49 + 343) + ... + 72013( 1 + 7 + 49 + 343)
=> P = 7 . 400 + ... + 72013 . 400
=> P = (7 + ... + 72013) . 400
=> P = (7 + ... + 72013) . 202 (đpcm)

Chọn C.
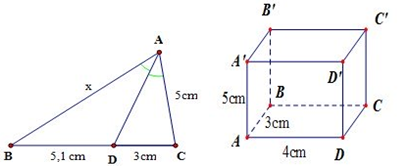
Phương pháp : Chú ý bình phương vô hướng bằng bình phương độ dài.
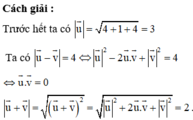

Đặt ưcln(n+3,n+4)=d(d€N*)
=>{n+3,n+4 chia hếtcho d
=>{4n+12,3n+12 chia hết cho d
=>4n+12-(3n+12)chia hết cho d
=>4n+12-3n-12 chia hết cho d
=>1chia hết cho d
=>d€ Ư(1)={ +-1}
Vậy n+3,n+4 nguyên tố cùng nhau
b) Gọi d là ƯC ( 2n + 3 ; 6n + 8 )
=> ( 2n + 3 ) \(⋮\)d và ( 6n +8 ) \(⋮\)d
=> 3 ( 2n + 9 ) \(⋮\)d và ( 6n +8 ) \(⋮\)d
=> [ ( 6n + 9 ) - ( 6n + 8 ) ] \(⋮\)d
=> 1 \(⋮\) d ; d \(\in\) N*
=> d = 1
Vậy ƯCLN ( 2n + 3 ; 6 n+ 8 ) = 1 => \(\frac{2n+3}{6n+8}\) là phân số tối giản.