Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Xét từng phát biểu:
(1) Đúng.
(2) Sai, đây là phản ứng khử.
(3) Đúng.
(4) Sai, với trường hợp este phenol như CH3COOC6H5 thì sản phẩm là 2 muối.
(5) Sai, có 3 N.
(6) Sai, tripeptit trở lên mới có phản ứng màu biure.
Số phát biểu đúng là 2.

Ở người, nồng độ glucozơ trong máu được giữu ổn định ở mức 0,1% => Phát biểu (1) đúng.
Khử hoàn toàn glucozơ bằng hiđro (xúc tác Ni, t0) thu được sobitol =>Phát biểu (2) sai.
Tơ xenlulozơ axetat thuộc loại tơ hóa học =>Phát biểu (3) đúng.
Thủy phân este đơn chức trong môi trường bazơ luôn cho muối của axit và ancol hoặc anđehit, muối của phenol,…:
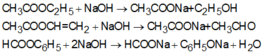
=>Phát biểu (4) sai
Glu (1NH2) , Lys (2NH2) =>Số nguyên tử N có trong phân tử đipeptit Glu-Lys là 3
=> Phát biểu (5) sai.
Từ đipeptit trở lên mới có phản ứng màu biure với Cu(OH)2 tạo dung dịch màu tím
=> Đipeptit không có phản ứng màu biure =>Phát biểu (6) sai
Các phát biểu đúng là (1), (3).
Đáp án A.

Chọn C.
(d) Sai, Thủy phân este đơn chức mạch hở trong môi trường kiềm luôn thu được muối và có thể có hoặc không có ancol.
(e) Sai, Số nguyên tử N có trong phân tử đipeptit Ala–Lys là 3

Chọn A.
(1). Đúng.
(2). Sai, Amilopectin có mạch phân nhánh.
(3). Đúng.
(4). Sai, Phản ứng thuỷ phân este có thể tạo ancol, anđehit, xeton,..
(5). Sai, Số nguyên tử N có trong phân tử đipeptit Glu–Lys là 3.
(6). Sai, Đipeptit trở lên mới có phản ứng màu biure.
(7). Đúng.
(8). Sai, Hiđro hóa chất béo lỏng trong điều kiện thích hợp thu được chất béo rắn.

HD:
FexOy + yCO \(\rightarrow\) xFe + yCO2
Trong một phản ứng hóa học, các chất tham gia và các chất sản phẩm phải chứa cùng số nguyên tố tạo ra chất.

Thầy rất hoan nghênh bạn Thịnh đã trả lời câu hỏi 2, nhưng câu này em làm chưa đúng. Ở bài này các em cần phải vận dụng phương trình BET để tính diện tích bề mặt riêng:
Sr = (Vm/22,4).NA.So. Sau khi thay số các em sẽ ra được đáp số.
E làm thế này đúng không ạ?
n(N2)=PV/RT=1*129*10^-3/(0.082*273)=5.76*10^-3 (mol)
Độ hấp phụ: S=n(N2)/m=5.76*10^-3/1=5.76*10^-3 (mol/g)
Diện tích bề mặt silicagel: S=N*So*J=6.023*10^23*16.2*10^-20*5.76*10^-3=562(m2/g)

phương trình dạng toán tử : \(\widehat{H}\)\(\Psi\) = E\(\Psi\)
Toán tử Laplace: \(\bigtriangledown\)2 = \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\)
thay vào từng bài cụ thể ta có :
a.sin(x+y+z)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))sin(x+y+z)
=\(\frac{\partial^2}{\partial x^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial y^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial z^2}\)sin(x+y+z)
=\(\frac{\partial}{\partial x}\)cos(x+y+z) + \(\frac{\partial}{\partial y}\)cos(x+y+z) + \(\frac{\partial}{\partial z}\)cos(x+y+z)
= -3.sin(x+y+z)
\(\Rightarrow\) sin(x+y+z) là hàm riêng. với trị riêng bằng -3.
b.cos(xy+yz+zx)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))cos(xy+yz+zx)
=\(\frac{\partial^2}{\partial x^2}\)cos(xy+yz+zx) +\(\frac{\partial^2}{\partial y^2}\)cos(xy+yz+zx) + \(\frac{\partial^2}{\partial z^2}\)cos(xy+yz+zx)
=\(\frac{\partial}{\partial x}\)(y+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial y}\)(x+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial z}\)(y+x).-sin(xy+yz+zx)
=- ((y+z)2cos(xy+yz+zx) + (x+z)2cos(xy+yz+zx) + (y+x)2cos(xy+yz+zx))
=-((y+z)2+ (x+z)2 + (x+z)2).cos(xy+yz+zx)
\(\Rightarrow\) cos(xy+yz+zx) không là hàm riêng của toán tử laplace.
c.exp(x2+y2+z2)
Đáp án đúng : A